PARTS OF
GILLEN
Someone recently informed
me that Gillen also uses the Arabic parts to produce numbers. This intuitively
makes sense to me. Only something that moves very fast and that depends upon
locality would account for the variety of numbers that might come out of---- conducted
in the various cities of Italy on the same day at the same time. Under Gillen's
scheme, each number has its own part and to determine them he uses
"modern" planets, too, not just the classical seven.
The first time I read
anything of the part of "anything" is from ACSM book. The only other
author that has written something is Jack Gillen. Although the actual mechanics
on how to apply it has been left out.
According to Jack Gillen,
all commodities, actually anything, has an Arabic part that indicates it's
trend. The only formula he ever gave was the part of Coffee although other
parts was mentioned without disclosing their formula.
The exact formula is left
to the reader to discover through research. What I've shown is how to find the
part of DOW which can be also be used for other commodities or stocks. The most
important criteria is follow-on test with other astro-events.
Testing with Saturn
initially was easy as there only a handful of them to test before testing the
other more frequent events. The natal chart also has a sensitive arabic part.
Although we are only interested in the ups and downs of an instrument, there
are other parts which describe the trend of other facet of life.
So based on repeated
tests the part of DOW from the rotation
chart is "asc+venus-sun".
> Based on using all available data from
1896, the Arabic parts for
> appears to involve the Sun and Venus using both the front and back
> formulas at the time of Jupiter/Saturn conjunction.
>
> The formula looks like this
>
> 1. asc+Venus-Sun
> 2. asc+Sun-Venus
> One of the body in the formula could be
the ruler of some sort.
The conjunction of two
slow moving planets especially when both are retrograde causes a unique problem
in pinning down the exact time of the conjunction. Depending on where you
look one could be out by several hours. With the ascendant every 4
minutes out is a degree off. When Saturn is used, this could mean being out by
potentially a week or more.
The basic idea was suggested by Pallicus in an
unpublished manuscript now in the
British Museum. They are points in the local sphere. The Parts can be
calculated in the daily motion only.
The Parts are normally launch from the Ascendent, but can also be launch from
the MC or the Descendant.
The Parts are estimated along the equatorial circle and then through the
passage degree formula their position is characterized on the
ecliptic.
Here a link where you will
find a calculation example
(according to Placidus)
http://www.cieloeterra.it/eng/eng.articoli.sorti/eng.sorti.html
In the reprint of the
Coelestis Philosophia of
1675, Francesco Brunacci e Francesco Onarati notice of the inadequacy
of the method of Placidus and of it they propose one new. They do not
speak to you express about hours but about equatorial distances.
ENGLISH TRANSLATION :
Marco Fumagalli
The hourly fate, the
true lunar horoscope.
(Phôs 2, June 2001)
Calculation of fate is
one of the most complex and controversial arguments of all astrological theory. The
method Placido Titi exemplifies in the Canon of the Part of Fortune,
at the end of his treatise on Primum Mobile (1657), can certainly
be termed a "cano" method, since it is based on equatorial arches and
not on the simple ecliptic distances of the method "vulgar". His
method, as he himself tells us, is what his friend Adriano Negusanzio has
reported to him, "highly skilled in astrological discipline according to
the true doctrine of Ptolemy." Negusanzio realized the inadequacy of
the vulgar method based solely on the celestial coordinates of the Sun and
Moon, without taking into account the local situation of the two astronauts. He
then conceived a different system that best responded to the well-known
Ptolemaic principle:
|
"The fortune fate, and day
and night, must be calculated according to the quantity of the number from
the Sun to the Moon, returning the equivalent distance from the horoscope
according to the sequence of the signs, so that the ratio and its own
configuration of the Sun with respect to the horoscope is also of the Moon
with respect to the fate of fortune, on which almost appears a lunar
horoscope »(3:11). |
Let's briefly summarize
the method of Negusanzio-Placido, which we have fully explained in the article
" The
calculation of the fate according to Placido Titi ". The
principle is as follows: Where the Moon is located when the Sun is in the
horoscope, that is the place of fate. To find the position of Negusanzio's
fate calculates the distance between the Sun and the horoscope in oblique
ascension and adds the straight ascension of the Moon. The result is the
straight ascension of the fate that will always be on the parallel of the Moon
declination.
ar ( ![]() )
= ao (Hor) - ao (
)
= ao (Hor) - ao ( ![]() )
+ ar (
)
+ ar ( ![]() )
)
If we apply this
calculation at the time of the rising of the Sun, we will find that the right
ascension of fate corresponds to that of the Moon. By placing the fate on
the lunar parallel we will have a total correspondence between the Moon and the
fate: it will dune from the Moon as many hours as the Sun is from the
horoscope, or zero. So we can say that fate is the lunar horoscope.
Limit of the Negusanzio-Placido
method.
This method therefore
responds perfectly to the Ptolemaic principle, but only at the rising of the
Sun. In fact, as soon as the Sun starts to rise above the horizon for daytime
motion, the Moon also moves and their hourly distance assumes different values. The
placid fate, on the contrary, remains almost fixed in the place where it was at
the rising of the Sun, moving only slightly, due to the motion of the Moon in
right ascension. This means that, during daytime rotation, Placido's fate
no longer maintains with the Moon the same time relationship that the Sun has
with the horoscope and ceases to be the moon horoscope. Let's demonstrate
what is said with an example.
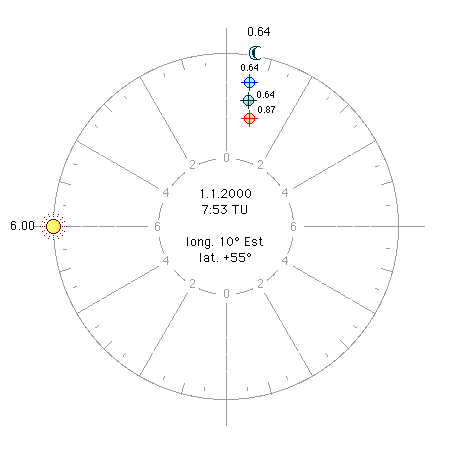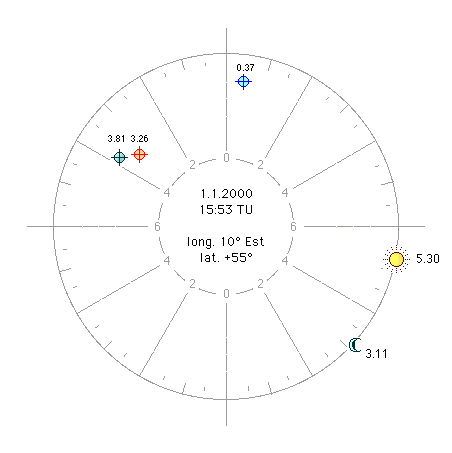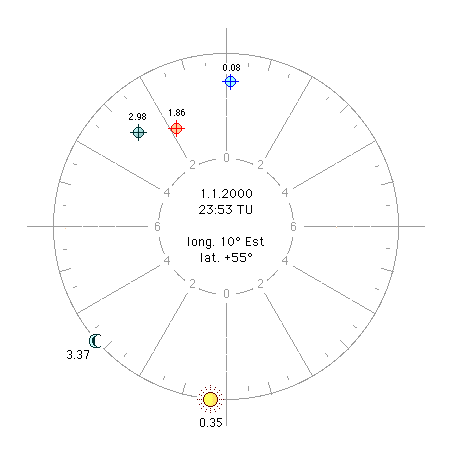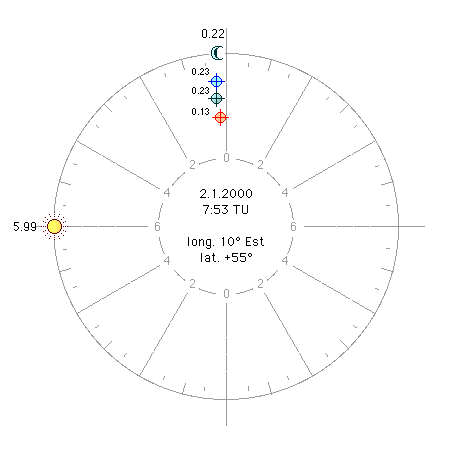
|
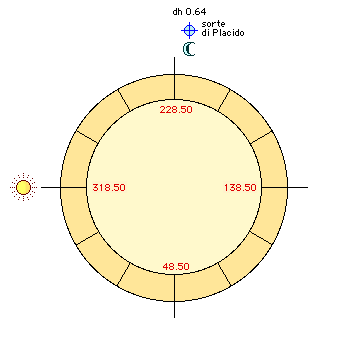
a1) Sun at the Horoscope - (Figure
1). Let's take this figure: 1.1.2000
hours 7:52:51 TU, pole + 55 °, long. East 10 °.Culmination 20 ° 56
'Scorpio, armc 228.50. ar
( Assigning the moon declination,
-10 ° 26 ', we find that the fate is from the middle ages 0.64 hours, in
ninth house, exactly like the Moon. The two luminaries are 6.64 hours
apart, and the fate is from the horoscope 6.64 hours. Correspondence is
perfect. |
Figure
1 |
|
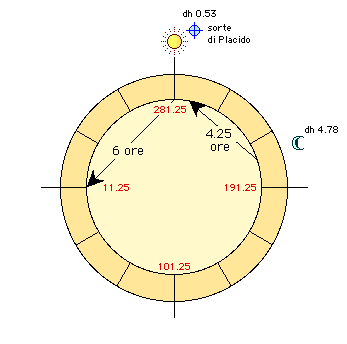
a2) Sun away from the
horoscope - (Figure 2). Let us now move forward in time,
for example, until the culmination of the Sun, at 11:23:15 TU. Culmination
10 ° 20 'Capricorn, arm 281.25. It rises 0 ° 27 'Bull, ao (Hor) 11.25. The
Sun is culminating in the mediocre; its longitude is the same as the
mediocre, 10 ° 20 'Capricorn; its ao is 318.64 (the equator level rising
to the pole + 55 ° along with 10 ° 20 'Capricorn). The Moon is 13 ° 01
'in Scorpio, latitude +5.18, declination -10.80, in seventh house, at a time
of 4.78 hours; its straight ascension (ar) is 222.15, declination
-10.80, daytime hours 12.36. Since the Sun culminates its hourly
distance is 0 and therefore the two luminaries distance between them 4.78
hours. The Sun is 6 hours from the horoscope and therefore we should
expect the moon horoscope at 6 hours from the moon. Let's see if it is
this way: ar
( Since the declination and the
temporal times are those of the Moon, we take the straight distance of the
fate, arsenal = 6.49, divide it by daytime hours 12.36, and we get 0.53,
hourly distance of the fate in ninth house. |
Figure
2 |
Placido's fate is only
4.25 hours from the Moon, well below the 6 hours we were waiting for. We
can not say that we have found the lunar horoscope spoken of by Tolemeo! What
happened? It happened that this fate, calculated on the basis of the steep
ascents at the pole of the region, remained almost fixed (in fact, it moved
slightly since the Moon moved a little in right ascension), while the distance
in hours between the two luminaries have changed considerably. So if we
look for the true moon horoscope, we will have to adopt a method that takes
into account this shift: we will have to adopt a time method.
The real lunar
horoscope.
A few years after
Placido's death, in the reprint of Coelestis Philosophia of
1675, Francesco Brunacci and Francesco Maria Onorati perceive the inadequacy of
the placid method and propose a new one. This is the time method. Brunacci
and Honorary do not speak of hours but of equatorial distances, which, as we
know, are the same thing.The calculation maintains the same structure but is
done entirely on the equator by working with the oblique ascension of the
horoscope and the mixed ascents (am) of the luminaries, ie
with the aoch in the ascending hemisphere and with the doch in the descending
one. What we get is in turn the mixed ascension of fate:
am ( ![]() )
= ao (Hor) - am (
)
= ao (Hor) - am ( ![]() )
+ am (
)
+ am ( ![]() )
)
Let's apply this method
to our example, 1.1.2000 hours 7:52:51 TU (see above):
|
Figure
3 |
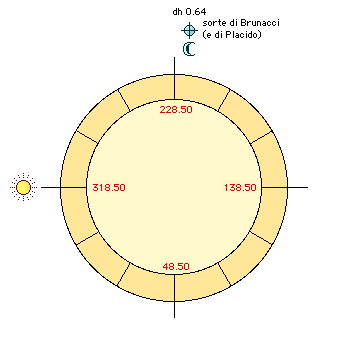
b1) Sun at the Horoscope -
(Figure 3). The mixed ascension of the Sun (in
this case, it is an oblique ascension to its pole, aoch) is identical to the
oblique ascension of the horoscope, or (Hor), 318.50, since the Sun rises and
its pole is + 55 °, like the one in the region. The Moon pole is 9.37
and its mixed climb is 218.85. Since the Moon is descending (it has just
past the meridian), it is an oblique discus (doch), at the 9.37 pole. We
then: am
( We immediately see that this value
is identical to the moon doch. Taking the distance of this point from
the meridian (armc - 218.85) we find a 9.65 arc which, divided by 15,
corresponds to a 0.64 hour distance from the meridian, into ninth house. Again the fate coincides perfectly
with the Moon. Therefore, at the rising of the Sun, we obtain the same
result as the Negusanzio-Placido method. Refer to Figure 3 with Figure
1. |
|
Figure
4 |
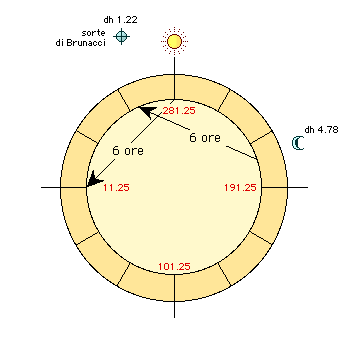
b2) Sun far from the
horoscope - (Figure 4). At the culmination of the Sun, the
aoch of the Sun is 281.25, identical to the straight ascension as it is on
the meridian where the pole is 0 °; the Moon pole is 49.47 and its mixed
climb (am) is 209.55. Since the Moon is descending, this is an oblique
discovery (doch) at pole 49.47. am
( This value surpasses the armc and
that means we are in the tenth home and not in the ninth. Then we take
the distance of this equatorial degree from the meridian (299.55 - armc) and
we find a 18.30 arc that divided by 15 gives 1.22, hourly distance of the
fate in tenth house. The Moon is in the seventh, at 4.78 hours from the
Middle Ages, and from the Sun. Summing up the distance of tithing
in the tenth, 1.22, we find that the Moon is exactly six hours from the fate,
when the Sun is out of the horoscope. We found the real moon horoscope. Compare
figure 4 with figure 2: Brunacci's "hourly" fate is 1.75 hours from
Placido's. Likewise, we can proceed with all
the other fates, always taking the ascents of the ascending point, the
disagreements of what comes down. |
Degree of passage.
The "hourly"
method of Brunacci and Honor involves a difference in how to find the degree
of passing of fate, that degree that passes at the same hourly
distance of fate and is taken as a reference for the attribution of planetary
dignities. Let us first remember how the degree of passage of placid fate
is found:
a) Placido's
fate . The method of Placido must proceed by attributing the
declination and ascending difference of the moon (dec, da) to the fate by
applying the formula of the poles dividing the ascending difference according
to the hourly distance of the fate (dh):
tan (P) = its (1/6 by dh) cotang (dec)
In our example (a2) we
will get the following result, knowing the declination of fate, -10.80, its by,
15.82, and its dh, 0.53:
tan (P) = its (1/6 x 15.82 x 0.53) cotang (-10.80)
P = 7.29
Now we find the degree
of passage ( theta ) with the poles of the poles (or
with the usual formula we also use for the cusps of the houses) by first
calculating the doch of fate (found in ninth house, therefore descending) that
we still do not know: doch ( ![]() )
= armc - 15 dh = 273.3. Let's proceed now with the formula:
)
= armc - 15 dh = 273.3. Let's proceed now with the formula:
|
tan
( theta ) = |
sin
273.3 cos
273.3 cos 23 ° 27 '+ sin 23 ° 27' tang 7.29 |
We find that theta is
equal to 275.93 or at 5 ° 56 'degrees of Capricorn. This is the ecliptic
degree that passes at the same hourly distance of Placido's fate (for this
calculation see also the article " The
calculation of the fates according to Placido Titi ").
b) Hourly
variety . With the time method we can not attribute the
declination of the moon to fate, indeed, we can not attribute to the fate any
declination. The hourly fate is not a point of the sphere (with
right ascension and declination), but rather a time zone , a
distance measured according to the motion of the hours (see figure 5). It
is in this very similar to the horizon and we could call it a horizon related
to the moon, a lunar horoscope. Just as all the points on the horizon
distance the same hours from the Sun, likewise all the points on the horizon of
the Moon, that is, all the points of the fate, distance the same hours from the
Moon. Then, in order to find the pole of fate, we could choose any point
in this circle, for example, that lies on the equator or on the ecliptic, and
operate according to its declination and its ascending difference.
But there is a more
elegant and simpler method, which does not force an arbitrary choice. Once
again the method is exposed by the Brunacci and the Ororate: it consists in
calculating the pole of fate considering its position in the house, according
to the distance proportional to the cusps. That is, if, for example, the
circle of fate is in tenths and we know its hourly distance, knowing that a
house has an hourly amplitude of 2 hours (or 30th equatorial), we can calculate
the pole (P) of the fate with the following proportion:
|
P
( |
(P2
- P1) dp1 2 |
where P1 and P2 are the
poles of the cusps of the house in which the fate is found: P1 is that of lower
value, P2 is that of higher value; (P2-P1) is the polar amplitude of
the house where fate is found; dp1 is for hourly distance from the cusp
closest to the meridian. Let's apply this method to example (b2); since
fate is in tenths P1 corresponds to the meridian pole, that is 0, and P2 is the
pole of the eleventh, 26.98. The lot is 1.22 from P1.
|
P
( |
(26.98
- 0) x 1.22 2 |
P ( ![]() )
= 16.46
)
= 16.46
Found the pole of the
fate we look for the poles of the poles to which degree corresponds the oblique
ascending 299.55 to pole 16.46. Or we use the formula:
|
tan
( theta ) = |
son
299.55 cos
299.55 cos 23 ° 27 '- sin 23 ° 27' tang 16.46 |
We find that theta is
equal to 291.05 or 21 ° 03 'Capricorn.
Conclusion.
After showing how the
two calculations lead to very different results, we can now reflect on the
different nature of these two varieties. Both originate from distances calculated
on the equatorial arches but Placido's fate has its own right ascension and its
own declination (that of the Moon), so it is a precise point in the
local sphere , while Brunacci is a time zone that
keeps the moon the same distance that the horizon has with the Sun; therefore
this fate is just like a moon horoscope, a moon horizon.Brunacci expresses this
concept very clearly:
|
"Now, fortune-telling should
not be described in the Moon's declination, but in the time zone in which the
calculus falls, as it has to be like a lunar horoscope. In fact, we consider the Sun's horizon not at the
point where it emerges, but in a circle whose track compares with the degree
of the zodiac, as is the constellations that coincide. Likewise,
in the circle of fortune, that degree of the zodiac that intersects the said
timeframe of the fate for the rule of oblique ascensions must be placed in
the theme to draw the governor of life out of the way Tolemeo teaches. " |
The hourly fate of the
Brunacci and the Ornate should therefore be adopted as a true moon horoscope
and the method must be extended to all other varieties. The difference
between the two methods is substantial and involves some very important
consequences, primarily in the use of directions:
a) as we have seen,
Placido's calculation maintains the time relationship at the moment of the
rising of the Sun and at this time fixes the fate at a precise point of the
sphere corresponding to the Moon's position; from this moment the fate
remains fixed, as a constant reflection of the Moon at that point, moving only
of the same lunar motion in right ascension; this means that fate is
almost regarded as a star, with its own heavenly coordinates. It follows
that it is possible to direct this fate in both directions, as a planet: in the
sense of succession of zodiac signs, and in the sense of daytime motion.
b) the hourly fate is a
circle, like the horizon. It does not have celestial coordinates, but only
one hourly distance and a degree of passage. The latter corresponds to the
point where the ecliptic intersects the circle, as well as the horoscope is the
point where the ecliptic intersects the horizon. Consequently, the
direction of the hourly sequence will be exactly the same as the direction of
the horoscope, or only in the zodiacal direction, and not in the opposite
direction: as well as the degrees of "zodiacal" directions ascend to
the horoscope according to oblique ascents or descend all 'west according to
disbelief, the same degrees will rise, or will descend, to the circle of fate
according to ascents, or discontents, oblique of that circle. No other
direction of the hour time is allowed.
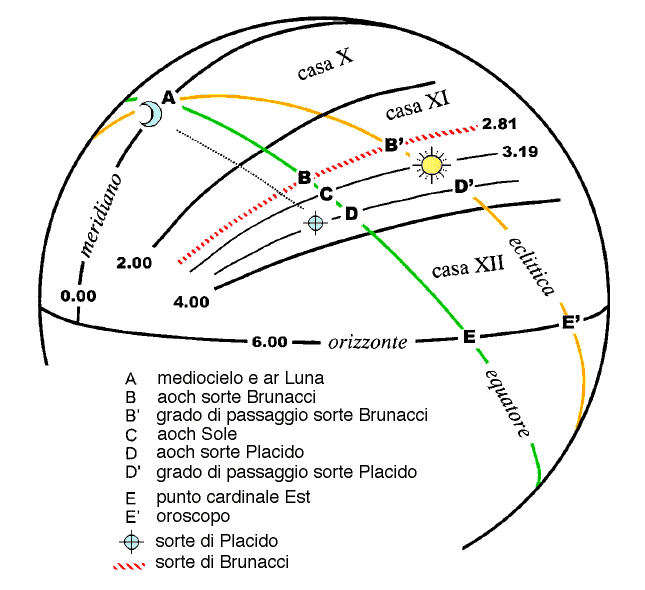
Figure 5
|
In this figure we see the sun in
eleventh house (DH 3.19) and the moon at the culmination (DH 0). Placido's
fate is on the parallel of the Moon's decline and falls into the eleventh
home, between the Sun Hours (3.19) and the twelfth (4.00). It is a
precise point of the sphere with its own coordinates. Brunacci's fate,
however, is the 2.81 hourly circle and is like a high horizon to distant from
the moon so many timeframes (2.81) as far as the horizon of the ball from the
sun is. In fact AB = 2.81 hours = 42.15 degrees equinoxial; CE = 6 -
3.19 = 2.81 hours = 42.15 degrees equinox. This is the fate that corresponds
to the lunar horoscope spoken by Tolemeo. |
Appendix.
We find it useful to
bring in an appendix an animated chart showing the movement of the different
fate: Placido, Brunacci and the "vulgar" movement. The Sun
performs a full rotation, at two-hour averages of average solar time, at the 55
° pole. Notice how the distance between placid and hourly occasions
increases with increasing distance between the sun and the horoscope.
|
this
animated image is taken from the 6th lesson of the Course |
If we had drawn this
figure for the 45 ° or 35 ° pole, we would have found minor differences between
placid and hourly fate, since these are reduced by approaching the equator. The
reason is clear: to the equator, the ascending difference is null and the poles
of the stars are all equal to 0 °, so it is no longer meaningful to speak of
ascents or oblique discontinuities with respect to the pole of the site (0 °)
or the pole of the 'astro (0 °): each point rises, culminates and slides along
with its straight ascension. All calculations are then merged according to
straight ascents and the Placido and Brunacci formula coincide: ar (Sorte) = ar
(Hor) - ar (sun) + ar (moon). By moving away from the equator of the
observation point, the ascension difference increases gradually, and thus the
difference between the two fates that reach the maximum values at each pole when the Sun is at the far western
point horoscope.
http://www.cieloeterra.it/articoli.sorteoraria/sorteoraria.html
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Marco Fumagalli The calculation of
the lots, according to Placidus. (Linguaggio Astrale
103, June 1996), english translation by Daria Dudziak |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
According
to the system of Placidus, the lots may be defined as the points of the local
space chart which, having the same declination as the point B, are as many
degrees away from it in right ascension (RA), as the point C is away from a
point A in oblique ascension (OA) and in the same direction. The points A and
B may be planets, house cusps or even lots; the point C is usually the
oriental horizon or horoscope (hor). The name and the astrological meaning of
the lot depend on the quality of the points A and B, on the basis of which
the lot is calculated: the lot calculated from the Sun to Saturn is called
the father's lot as these two celestial bodies are the significators of the
father. Two general formulas for the calculation of the lots may be expounded,
one which makes possible to find its AR and another its AO: OA (hor) - OA (A) + RA (B) = RA lot The
two points have to be reversed between them if at the moment we are
considering the Sun is under the horizon: for example in order to find the
mother's lot in a diurnal figure we take Venus as the point A and the Moon as
the point B, but if the figure is nocturnal we do the opposite. On the other
hand several lots do not change from the day to the night as, for example, that
of marriage. We show as an example the calculation of the Moon's lot, also
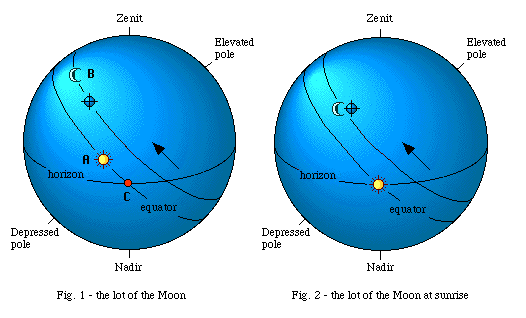
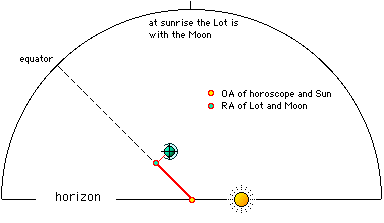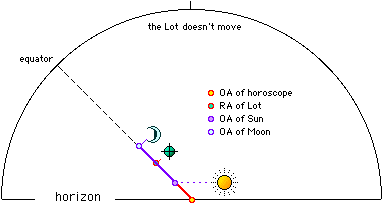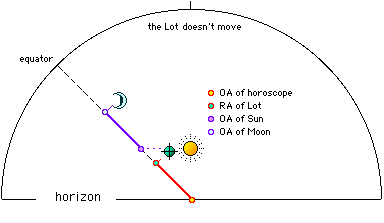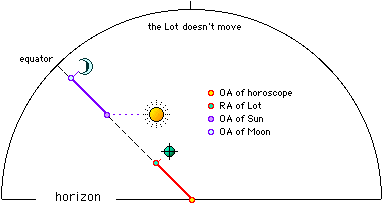
called Tychê or Part of Fortune and indicated with the following symbol by day: OA (hor) - OA ( The
following two figures should explain the principle on which the calculation
of the lunar lot and of all the other lots is based (the small arrow
indicates the diurnal motion of the local sphere):
As
I wanted the drawing to be as clear and simple as possible, I have left out
the ecliptic in the figures and I have placed the Sun on the equator, at the
autumnal equinox. In the figure 1 we see how the lunar lot is situated at
exactly the same point where the Moon would be if by turning the sphere
counterclockwise we made the Sun rise at the eastern horizon (figure 2). For
this reason it was called "the lunar horoscope" seeing that its
distance from the Moon measured in equatorial degrees or in time is equal to
the distance between the real horoscope and the Sun (C-A).
Therefore
it is obvious that, like the horoscope and the house cusps, the lots are the
points of the local sphere: they express a relation between two points
calculated only in virtue of the daily motion and of the equatorial arches. Let's
see now a complete example of calculation beginning from the data of a
diurnal geniture: Milan, the 14th of April 1956, 10 hour and 35 minutes. It
culminates in the midheaven 25°03' of Pisces which right ascension, RAMC, is
of 355°28'. The oblique ascension of the horoscope, OA(hor), is of 85°28':
The
Sun is in Aries at 24°24'49",and the Moon is in Gemini at
7°;07'48", the north latitude is of 0°09'36". Their right
ascensions (RA), declinations (decl.) and oblique ascensions (OA) in Milan
are indicated below; we cite also the ascensional difference(AD) of the Moon
or the difference between its RA and its OA which will be useful for us
later:
Now
we have at our disposal all the elements necessary for the calculation of the
position of the lunar lot: 1.
first of all we start with finding the right ascension (RA) according to the
method we explained for a diurnal geniture :
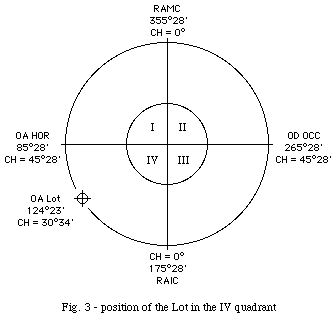
2.
afterwards as we know the RA of the lot, we can calculate its distance in
right ascension from the nearest meridian (MC o IC) which is called
"right distance" (RD) or "meridian distance". From the
right ascension of the lot we see immediately that it is under the horizon,
in the IV quadrant, between the horoscope and the Imum Coeli (IC), since its
RA is higher than the OA(hor) and lower than the right ascension of the Imum
Coeli: RA(IC) = RA(MC)+180 = 175°28'. Therefore its right distance RD should
be calculated from the Imum Coeli:
3.
We proceed now to calculate the temporal hours (TH) of the lot that in this
case (diurnal nativity) will be the same of the Moon, seeing that the lot,
having the same declination shares the ascensional difference (AD) and the
temporal, diurnal (THd) and night-time (THn) hours with the Moon.; therefore
the AD of the lot is 23°49'00". Since the AD corresponds to the
difference between ascensions (oblique and right) that takes place between
the rising and the culmination in the space of a quadrant (equal to a quarter
of the whole day, therefore to 6 temporal hours), if we divide by 6 this
value we get the quantity of equatorial degrees which added to or subtracted
from 15° (equal to an equinoctial hour: 15° x 24 =360°), expresses the value
of the single temporal , diurnal and night-time hour. The temporal hours will
always be higher than 15° in the hemisphere situated to the north of the
equator (positive declination), while they will be lower than 15° in the
hemisphere south (negative declination). The declination of the Moon and of
the lot is positive therefore the calculation is the following:
4.
Now we can find the hourly distance (HD) of the lot, dividing the right
distance for the temporal nocturnal hours of the Moon (THn). We use the
nocturnal hours since we already know that the lot is under the horizon; if
instead it had stayed above we would have calculated the right distance from
the Midheaven and we would divided it for the diurnal hours.
In
this moment the lot can already be inserted in the figure and we can
calculate all the aspects that it receives in the world or according to the
hourly distances. However we still have to find the ecliptical degree in
which the lot should be registered that serves us to know which is the ruler
of the lot or the planet that has more dignity on that degree. If we knew the
equatorial coordinates of the lot (RA and decl.) we could easily find the
ecliptical coordinates (longitude e latitude) by means of the trigonometric
formulas of conversion between orthogonal coordinates. Nevertheless, since
the lot, like fixed stars , does not have its own motion in the sky, but it
is a point of the local space chart, we do not have to take its degree of
ecliptical longitude (which is a coordinate of the celestial sphere), but its
degree of passage in the local space chart. The degree of passage of a point
in a space chart is not other than that degree of the ecliptic that in a
datum moment transits to the same hourly distance from the meridian in the
same quadrant. That point of the ecliptic that in the IV quadrant will have a
hourly distance of 3h24m21s from the IC will be therefore the degree in which
we should register the lot. We will see now how to find it. 5.
First of all we have to find the oblique ascension (or the discension) of the
lot in its own circular chart (OACH-ODHC). Between two consecutive angles of
the local space chart there is always a distance of 90° of equator, equal to
6 temporal hours (figure 3) and the OACH or the ODCH expresses the position
of a star along this semi-arc . A star placed, for example on the horizon is
always 6 hours away from the meridian equal to equinoctial 90° and it still
has to cross all his diurnal or nocturnal semi-arc.
In
this distance covered the star "consumes" gradually its ascensional
difference which is maximum at the horizon (HC = 45°28' in Milan) and reduces
to zero on the meridian (CH = 0°), where its OACH-ODCH is equal to its RA
since the circualr chart is equal to 0°;. If we add 30° (equal to one HD of 2
hours) to the RA(MC) we get the OACH of the XI house and if we add other 30°
to this we find the OAHC of the XII house: this is the principle of the
Placidean domification. On the basis of the same principle if we multiply the
HD of a star for 15 we get an arc of equator which added to or subtracted
from the RA of the nearest meridian make possible for us to find the OAHC or
the ODCH of the star, depending on the fact that it is east or west of the
meridian. In our example:
6.
Now we have to find the horary circle (CH) or the "pole" of the lot
by means of the following formula: tang CH= sin (1/6 ADmax HD) cotang eps,
where eps means the obliquity of ecliptic (23°27') and the ADmax means the
maximum ascensional difference to a given elevation of the pole (phi). The
latter may be found with the following formula: sin ADmax = tang eps tang
phi. Since in Milan phi is equal to 45°28', the ADmax is 26°09'41", 1/6
ADmax is equal to 4°;21'37", and the horary circle (CH) of the lot is
30°34'35": tang CH 7.
finally we calculate the ecliptic degree of transit (theta) of the lot with
the following formula: tang theta = sin OACH: (cos OACH cos eps - sin eps
tang CH) that in our case gives 12°22'56" of Lion as result:
theta |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
http://www.cieloeterra.it/eng/eng.articoli.sorti/eng.sorti.html