Path Curves

A path curve is a projective transformation of space creating the simplest possible curve. It was one of Lawrence Edwards many discoveries that path curves very accurately describe the form of the buds of a comprehensive range of species.

Edward worked with actual measurements to see if he could find a better equation to describe the variations between actual measurements of plants and the statistical results created by existing math models of growth.

His first work was with eggs, the heart and the uterus.

His tests looked at consistency rather then the mean radius deviation, calling this a lamba parameter. The following diagram shows the meaning of this parameter:

The numbers are the lambda parameter, tending to infinity for a cone. The negative values yield vortex forms instead of buds. The bottom row shows eggs with the same lambda but with differing steepness-of-ascent of the spirals. This is controlled by a second parameter designated 'epsilon', which is 0 for horizontal circles and infinite for vertical profile path curves (see Reference 1 or Practical Path Curve Calculations for the maths).Source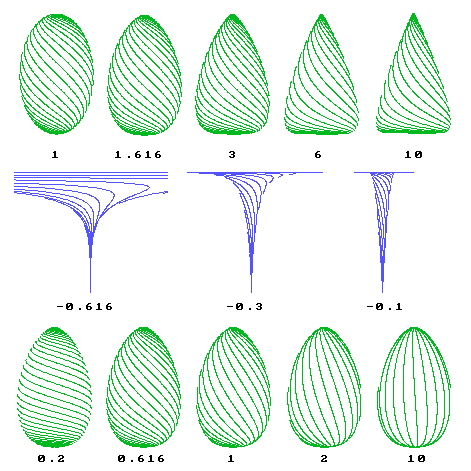

Questions he was asking:

1. Do all buds of a particular species such as the rose have the same lambda, or within what limits?
2. Is the goodness of fit any indication of the vitality of the plant?
3. The opening of buds has a certain "gesture" in the evolution of the lambda value. What is its significance?
4. Is there a way to describe the asymmetries in actual growth?

This is an excerpt from the site THE BUD WORKSHOP which goes into the topic with great depth. These extracts are for archival purposes, please see the orignal site which is full of much valuable material.

"Edwards' research is the first and only one to have, from first mathematical principles, successfully described any biological form. All other attempts at precision are essentially—and merely—statistical (norms are not principles). "

See also

• Beyond measure: a guided tour through nature, myth, and number By Jay Kappraff, from New Jersey Institute of Technology.

One Dimension	The moving point traces an invariant path curve This tracks a point as it steps across a plane. That track must represent the combination of two linear measures. This is Two Dimensional, as it is confined to a plane.
stepping a point along a line	Stepping a point along a line When we step a point along a line, we have recourse to two directing points and an intermediate line. The result is a pair of conjugate, linear measures in the line, between two invariant end-points that divide the line (i.e., points that cannot be stepped, or, if stepped, step exactly to where they are).
Two Dimensions	Two Dimensions When we step a point across a plane, we have recourse to two stepping lines, and our stepping point in the plane is at their intersection. Our lines rotate in points, which are the vertices of a triangle, and are guided by linear measures in the sides of that triangle, and the result is a path curve in the plane. The sides of the triangle cannot be stepped, so are invariant, and are functional infinities for the stepping lines. Accordingly, the entire triangle is invariant.
Three Dimensions	Three Dimensions When we want to step a point across the whole volume of space, we must have recourse to stepping planes, and the stepping point will be at their intersection. Three planes intersect in a point, so we must have three stepping planes.
Three Dimensional Planes	Three Dimensional Planes Four general planes form a tetrahedron. They intersect by triples in 4 points (vertices) and by pairs in 6 lines (sides).
Outside and Inside	Outside and Inside The four planes "enclose" volumes of space. That is, they divide the volume of all space into five volumes.
Three Dimensions	Three Dimensions We see that any one of these six could be a line in which a stepping plane might rotate, and that while six are available, three will do for tracking our point as it steps through the volume of space. Three such are shown one at a time on the right. The facets of the tetrahedron intersecting in a given line-of-rotation will be the planes of the corresponding functional infinities for the rotating plane. The rotations are guided by (independently determined) measures in the sides opposite to, and skew to, the sides in which the planes rotate.
The Path Curve	The Path Curve The result is a path curve moving in the volume of space—that is, in three dimensions—from one vertex of the tetrahedron to another, and avoiding the other two vertices.

---