A Day is G!

As William Blake, said, “to hold the universe in a grain of sand, and eternity in an hour!” Well, indeed Nature is fractal, and it seems the fundamental frequency of our harmonic scalar explorations just happens to be a Day. Bold claim – which I’ll explain below. All the vibrations and music we make naturally are sub-harmonics of that fundamental beat. The World turns, and we sing.

That’s not how the generally accepted, Western, A = 440 vibrations-per-second, non-harmonic, Equal Temperament scale works. And that’s why ultimately when we listen to nearly all commercial music, the message we’re actually receiving is one of dissonance with Nature.

Back to the Day. It makes sense – we live on a rotating vortex of energy which emits an electro-magnetic and gravitation field, (which I just happened to detect while using a frequency generator in 2016) at the frequencies of 5.4 Hz (F), 10.8 Hz (F) and 7.2 Hz (B-flat).

And it turns out that the 3rd harmonic below that B-flat is an E-flat which corresponds to one beat every ancient “Helek”. The ancient Hebrew measure of time (the Helek) was 3.333 recurring of today’s seconds – which is the time it takes the Earth to rotate 1/72nd of a degree. One beat per Helek corresponds to 0.3 vibrations-per-second (also known as Hertz (Hz)). And 0.3 Hz just happens to be an E-flat, exactly the 3rd harmonic below this same B-flat.

(What do I mean by “3rd harmonic below”? Basically, the frequency that is 3 times slower than the B-flat. So, if B-flat is 7.2, then 7.2 divided by 3 = 2.4 Hz. And the octaves of E-flat are 0.3 Hz -> 0.6 Hz, 1.2 -> Hz -> 2.4 Hz). And there is a measured peak in the Earth’s electro-magnetic field at 9.6 Hz (octaves 2.4 Hz -> 4.8 Hz -> 9.6 Hz)).

So, we have 3 frequencies we can be pretty sure are emanations of the physical energy field of the Earth.)

Let’s keep going because we haven’t talked about the Day yet: The frequency of one Earth rotation every 24 hours (or 1 vibration every 86,400 seconds).

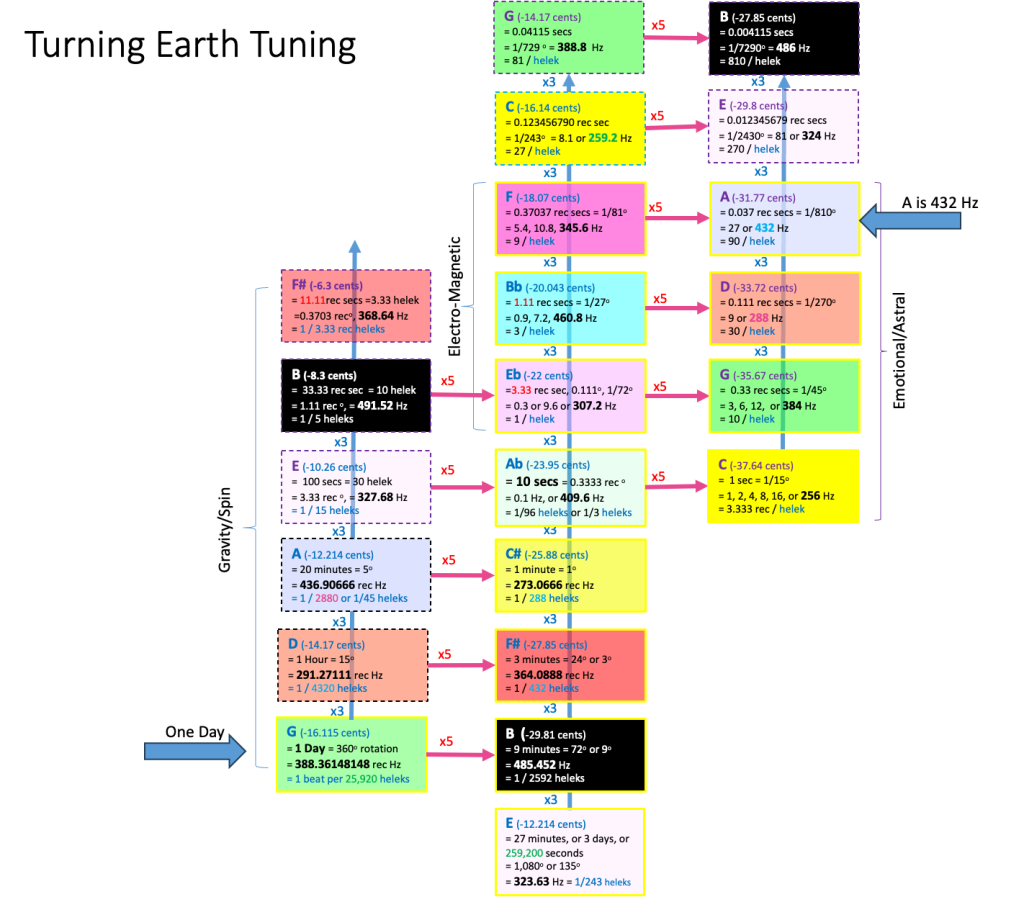
Based on this notion that a Day – the rotation of the Earth itself – might be the origin of these harmonics – here is an extrapolation of the frequencies, starting with the number of seconds in a day, (in the lower-left corner in the diagram above):

· 60 seconds x 60 minutes x 24-hours = 86,400 seconds per day (= 43,200 secs in 12 hours, for those who like to see the number 432)

· So, one beat per day = 1/86,400 seconds = 1.15740740 x 10^-5recurring vibrations per second (Hz)

· Which, if you octave it up a lot (multiply by 2, many times) = 388.36148148 recurring Hz.

Let’s take a quick recap of the harmonic and mathematical tools available to us:

· Octaves: The ear hears double the frequency of a note as an “octave”, e.g. perceptively the same note, only lower or higher. Multiply the frequency of your note by 2 to get an octave above, divide by 2 to get the octave below. For those of us old enough to remember, the bass-lines of My Sharona, and Thank You (Falettinme Be Mice Elf Agin) – or Some-Where Over the Rainbow.

· 3rd harmonics:

· Like it says on the tin, if you multiply the frequency by 3, you get the 3rd harmonic above. With a guitar string, this is what happens when you touch it 1/3 of the way along its length – it vibrates in 3 nodes, each vibrating 3 times faster than the original notes.

· The 3rd harmonic corresponds with going Do-Re-Mi-Fa-So, which is the 5th note in the Western major scale so they call it the “Perfect 5th” – which is confusing, but there you go. e.g. Twinkle-Twinkle Little Star. Conversely, dividing by 3 gives the 3rd harmonic below

· 5th harmonics:

· And if you touched your vibrating guitar string 1/5th of the way along, you would get 5 nodes each vibrating 5 times faster than the original. Multiply your frequency by 5 . This 5th harmonic corresponds to Do-Re-Mi, and is therefore called the “major 3rd” interval in Western music – ‘cos its the 3rd one.

So, these are our harmonic building-blocks. Yes, harmonics form at the 7th, 9th, 11th harmonic – actually on all whole numbers (that’s why primary numbers, and why Eddie Van Halen can get micro-harmonics all over his guitar neck), but they get progressively weaker, so the harmonics we hear primarily are the octaves, 3rd and 5th harmonics. And it’s this basic sonority that we seek in a musical scale: if these harmonics are clashing with one another, we’re going to feel that dissonance quite strongly.

So, let’s use these three harmonic tools to explore the harmonics of a Day.

As shown above, we have our Day as equivalent to a G of 388.36168168 Hz (1 beat per 86,400 seconds and octaved up by multiplying by 2 lots of times):

The 3rd harmonic is the strongest after the octave.

· The “3rd harmonic of a Day” = 24 hours / 3

· = 8 hours;

· The frequency is 3-times faster. So, multiplying a G of 388.36 Hz by 3 gives us the 3rd-harmonic above (=1,165.08504504 Hz, which if we divide by 4 to go down a few octaves = D of 291.27111 Hz.

· This D is illustrated in the chart above, as the D directly above the G in the lower left-hand corner.

· Because in harmonics, dividing or multiplying by 2 gives you an octave, this D frequency for 8 hours can be octaved up to 4-hours, 2-hours, 1-hour, half-an-hour, 15 minutes, and still be this D.

A Day corresponds to a complete turn of the Earth: 360 degrees. So, in the chart above I’ve also included the number of degrees, and the portion of the day in minutes which each musical harmonic represents.

In this way, we can find “geo-harmonic”, 3rd-harmonics in the left-hand column: G, D, A, E. I call these the “Geometric frequencies” because they’re all directly based on our rotating Earth.

Then, the other strong harmonic is the 5th-harmonic (central columns). Let’s see what happens when we take the 5th harmonic of “a Day”:

· The 5th harmonic of G is B (do-re-mi)

· 388.36 Hz x 5 = 485.452 Hz (after octaving it down)

So? Well, as it happens, when we extrapolate downwards in 3rd harmonics from the “phenomenal frequencies” (from the B-flat and E-flat we know, down through E-flat, to A-flat, C-sharp, F-sharp to B, going down in 3rd harmonics (divide by 3), as shown in the centre column, above, this is the exact same frequency that we get for B based on the geo-harmonic G in the left column (485.452 Hz). They exactly connect!

So, there it is Ladies and Gentlemen – the “phenomenal” frequencies that I experienced (as shown in the middle column) directly connect with the frequency of the Earth rotating once a day.

In other words, this confirms that the B-flat and F frequencies I had found are electro-magnetic resonances of the Earth’s rotation and its magnetic field.

And going the way other way,, the “geometric” frequencies generated from a Day exactly meet up with the harmonic series from the “phenomenal frequencies” (F, B-flat, E-flat). Seamlessly!

Coincidence? Well, no. Clearly, there are electro-magnetic, harmonic, vibrational “nodes” that emanate from our planet’s daily rotation, and which produce the harmonics I measured for B-flat and F.

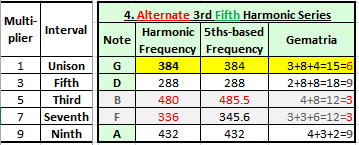
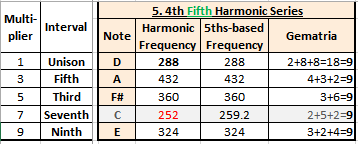
In the chart above – I’ve shown the 3rd-harmonics, going vertically – and the 5th harmonics, going sideways – and this includes a 3rd column where, by the way, we get another A at 432 Hz, and another D at 144 or 288 Hz. We’ll talk about those later.

The remaining trick then is to know which notes we are pulling from where in this harmonic matrix and to construct musical scales that resonate with specific aspects of the divine geometry.

e.g. Do you take the E from the first/Earth column (327.68 Hz), or from the second/magic column, or from the 3rd/heavenly column?

If we create our binaural beats based on these frequencies, our brains will be attuned – give this one I created a try, or this. Binaurals rely on headphones or stereo-speakers to deliver two different frequencies to your left and right ears, and your brain has to assimilate this information. I wonder if it will help remedy migraine headaches.

· I sometimes sleep with a 9.6 Hz magnetic resonator under the mattress, corresponding to E-flat, above. It brings on lucid dreams, and muscular relaxation!

· If our music and discourse are made against this fabric of sonority, we will be in-sync with the bird- and animal-song; we will hear what they are saying in the context of what it is – a hymn to the creative wonder that gives us life every moment of the Day!

When I took this following recording of Beethoven’s Moonlight Sonata which I tuned on my computer to play only these exact frequencies, out into the fields, it seemed like the Birds and the Sheep were just singing along all the time: I just happened to show up with a piece of music which was based on the same musical scale they were singing to already!

A day is a day. That may be the only thing left in our lives which cannot be re-construed, twisted and theoriticised by propaganda (I’m sure the Establishment would like us to live permanently in the Meta-Verse (AKA Matrix) where they can manipulate time itself, but that’s not going to happen). Take this piece of music out into the fields, and enjoy!

Alternative Frequencies

· In the right-column, we can generate alternative frequencies for G, D, A, E and B. And I’ve tried to highlight these “alternative flavours”in the same colour – e.g. E in purple. Potentially, for micro-tonal music, you could have an instrument with more than 12 notes per octave, and have multiple versions of these notes – and probably that’s what singers do. But for instruments with frets or hard-tuning like the pinch it’s a lot easier to keep it simple with just 12 notes per octave – and on the guitar, that’s what bends are for!

· Note, that these “upper” frequencies for G, D, A, E correspond to Zarlino’s frequencies in the 1500s, and the frequencies which enthusiasts for music based on A = 432 Hz generally espouse.

A Is Not 432 Hz

In the recording above, A is 436.90666 Hz – taken from the first column of 3rd-harmonics of the Day. In this next recording, the A is taken from the 3rd column above, two 5th harmonics away from the first column. You can decide which you prefer.

Earth Tuning with A = 432 Hz

Seconds and Helekim and Geometry

Just one thing to note is that some of these numbers are familiar, “cosmic” numbers in the Vedas, the New Jerusalem, Plato’s Magnesia, John Michell’s Dimensions of Paradise, etc., but I want to mention that there’s a hidden prejudice in our modern thinking, which is that we think everything is about the Second: Hertz is vibrations per Second. But, for the ancient Hebrews and Babylonians who developed the sexagesimal counting system – the unit of time was the Helek – equal to 3.333 recurring of today’s seconds; and not the second.

So, does the number 432 appear in Earth harmonic scale anyway even if we don’t make A=432 Hz? Yes, it does:

· 432 beats per Helek = 432 / 3.33333 seconds = 129.6 Hz. And what note is 129.6 Hz? It’s not an A, it’s an octave of C at 259.2 Hz

· Also, as it happens, there are 25,920 Heleks in a day (3.3333 seconds x 25,920 = 86,400 seconds (there’s that 432, 864 number again). So, 432 is important, but it may refer to C rather than A.

(John Michel is an excellent, readable source for information about the amazing coincidences of size, distance and proportion which mean that Pi can be derived from the ratio of the Earth to the Moon, how the Moon is sized and distanced so perfectly in relation to the sun that it precisely blocks it out in an eclipse, etc.; and amazing coincidences of how the same harmonic numbers we see here translate to the numbers of stades, furlongs and Egyptian feet necessary to span the Earth’s equator. Evidence of the harmonics of balance being foundational to our universe, and something never taught in today’s schools! )

We mentioned that there are 25,920 Heleks in a Day. There are also 25,920 years in the Great Year (the time it takes the precession of the Earth’s equinox to complete the tour of all 12 areas of the zodiac). So, the significance of 432 viewed with the ancient metrology of the Helek instead of the Second, shows itself more in the C-note as being of cosmic significance, than the A.

· Similarly for 288: Instead of 288 beats per second as a D, 288 beats per Helek = 288 / 3.33333 seconds = 86.4 Hz. And what note is 86.4 Hz? It’s not a D, it’s an octave of our magic F at 345.6 Hz

It’s not for nothing that the size of the “enclosures” at Gobekli Tepe, and the distances reported for moving stone with sound correspond to the wavelengths of the frequencies for B-flat, F and C. They are “sacred” resonances because they align with the very tissue of our conscious planet, and our experience of it.

Guitars are tuned like the Day!

Funnily enough, the open notes on a guitar are tuned to the 3rd harmonics emanating from the Day/G in the lower left-hand corner of the diagram. G D A E B. (tuned as E A D G B E). Even more interesting is that we derived all of these as 3rd harmonics, except for the G to B, which is 5th harmonic (going horizontal on the diagram above); and on standard guitar tuning, G to B is the only string relation based on the 5th harmonic. Perhaps there is something fundamental in the way a guitar is tuned that has somehow been passed down through the ages.

Other Observations:

· At C-sharp in the diagram, it corresponds to both 1-minute, and 1-degree.

· B-flat corresponds to 1.11 seconds. There is an increasing number of people who find that most of the time when they look at a digital clock it is showing 11 minutes, 22 minutes, 33, 44, 55 minutes past the hour. Perhaps then this is a harmonic event making itself known.

60-based counting, vs 64-based counting:

The ancient Babylonians worked out our 60-based counting system. 5 x 12 is 60; 12 can be derived from 3, 4, 6, etc. In the guitar-string example it works well, because when you touch your finger at various whole-number divisions of the length of the string, you hear the harmonics that make up the fundamental sound of the string played open. And the strongest harmonics are divisions at 2, 3, 4, 5, 6, 7, 8, 9 of the string length.

But some have posited that the Ancients got it wrong: there are, for example, 64 codons in DNA, 64 hexagrams in the I-Ching, and, of course, 64 is a binary number: 2, 4, 8, 16, 32, 64. One extension to this idea is that C should be 256 Hz (because 64, 128, 256), instead of 259.2 Hz from the middle column as the 3rd harmonic of F. (Whereas C at 256 Hz can be derived as the 5th harmonic of our Ab frequency (0.1 Hz x 5 = 0.5 Hz, which if you multiply by 2 gives you octaves of 1 Hz, 2, 4, 8, 16, 32, 64 Hz, etc.)

Notice though that, when viewed as vibrations per Helek, E-flat can be one vibration per Helek – or one vibration per 64 Heleks as it’s octave (1, 2, 4, 8, 16, 32, 64). E-flat, as one vibration per the Ancient unit of time provides that binary aspect to the sonic pattern, without having to distort C as 256 Hz.

As DNA has 64 codons, perhaps there is an interesting health opportunity with the use of E-flat as a healing frequency. As I mentioned, I use an electro-magnet under my mattress, set to E-flat (at 9.6 Hz) and I do seem to wake up refreshed. (The one I use, programmes in an hour of B-flat (14.4 Hz) at the end, so you are bought out of deep gamma. If I get up before that part of the programme, I’m pretty groggy!)

So, go to this section on Harmonic Instrument Design in order to play your music with these “Earth” harmonic frequencies.

https://harmonicsofnature.com/a-day-is-g/

Let’s cut to the chase.  What if there was an underlying vibration that is at the foundation of the universe and all music?  Well, I believe there is, and it’s 7.2 Hz.  Read on for a compilation of evidence of why this seems to be the case, and how to harness it for making your own personal music in harmony with all of creation.

INTRODUCTION

The internet is full of information about sound as a healing energy.  We find debates about whether the “A” note should be tuned to 440 Hz or 432 Hz; about the healing qualities of the “Solfeggio”; videos for “binaural mind entrainment”; discussions on the correspondence between color and music; explanations of “equal temperament” vs “just intonation”; theories about the vibratory qualities of the great pyramid; the vibratory foundations of DNA; the correspondence between the angles of the Platonic solids and musical frequencies – but when we try to put all this together it doesn’t seem to gel into a cohesive pattern of actual frequencies, notes and keys to play in order to be in tune with the universe.

So, the question for me is:  Is there a foundational vibration – and related musical key which would provide the most benefit – the most connection to ourselves and each other, to the natural World around us and the cosmos we live in?

I spent about five years thinking that one key or another was “the magic key” – tuning to different fundamental frequencies, playing out live – jud(ging audience reaction, recording bird-song and crickets and trying to play along on the guitar, waking with songs in my head and humming them into my iPhone. Then, luck rescued me from a lifetime’s quest one night in early 2016 in a hotel room in Johannesburg.

I had thought during dinner of playing some ultra low frequencies on a tone-generator app I had on my iPhone through the new Bluetooth headphones my sister had given me for Christmas – just out of a perverse desire to hear something weird and fundamental.  As I was dialing through these low frequencies, I noticed something strange – as I turned the dial to make the tone lower, there was another whooshing-thumping sound that was speeding up – until I reached a point at 10.8 Hz where the whooshing stopped – and just sort of hovered there.

My video of the “sonic still-point” phenomena.

Then, turning the dial further to the left – to make the frequency slower and lower still – I noticed that the whooshing once again was speeding up – and that it then slowed down again at 7.2 Hz.  “That’s curious” – thought I.
I turned the dial further to the left – again, the whooshing sped up again and then once again slowed to halt at 5.4 Hz.

I then realized that 5.4 Hz is half of 10.8 Hz – this phenomena was occurring at two octaves of the same note: an F.  And that 7.2 Hz happens to be exactly the musical “fifth” below 10.8 Hz:  (7.2 Hz x 3/2 = 10.8 Hz).

As it turns out, these two frequencies (5.4 and 7.2 Hz) are respectively very low octaves of the notes F and B-flat – from a “just intonation” scale based on this B-flat frequency – which also happens to position A at exactly 432 Hz.

(Interestingly, this phenomena cannot be perceived for sub-octaves of A=432 Hz (e.g. 6.75 Hz) – which indicates that B-flat and F are the source from which other harmonics are generated – and not A, as western musical convention might suggest.)

Besides the coincidence of the psycho-acoustic effect of these frequencies and the fact that they harmonically coincide with the body of knowledge around A = 432 Hz, I have discovered other intersections between these vibrations and aspects of art and science.

For example, it turns out that the “Solfeggio” – the collection of Gregorian micro-tonal frequencies which have been passed down in secret – are not a series of “magical tones” that impart healing on their own, but actually “difference notes” which when played in combinations of two or more Solfeggio notes at the same time, produce “difference” notes which correspond closely to the “magic” harmonic scale based on my B-flat and F frequencies.  The secret that was passed down through the millennia seems to be a big sign-post that says, “here are the actual notes you should be playing!”  I’ve documented this exploration here.

Meanwhile, NASA has recorded the sub-audio hum generated by black holes – which turns out to be an ultra low octave of B-flat.  I have also come across anecdotes from published writers and personal friends of musical notes that seem to “hang in mid-air” (also B-flat).  It turns out that the frequencies I discovered also correspond to “divine” numbers (54, 72, 108) from ancient Hindu texts; and I’ve found personal satisfaction in discovering that some of my favorite music from childhood happens to align with the harmonic series generated by these frequencies.

These coincidences and overlaps of knowledge have given me increasing confidence that I have stumbled across some fundamental and forgotten knowledge about the vibrational fabric of our universe – and, it seems to me, what better way to participate in “the music of the spheres” than to tune your instrument to it!

So, this blog is a collection of personal experiences and information I’ve pulled together which seem to support this discovery.  Please share your own experiences on the blog, or send me an e-mail.  It would be great to collect these shared experiences together.

Here we go:

THE PROBLEMS WITH WESTERN MUSIC

Why does some music resonate with our essential being, and some leaves us cold, dissonant, upset or even angry?

· Rhythm? Sure.  “it don’t mean a thing if it ain’t got that swing” !

· Harmony? It will certainly spruce up a simple song, and give it depth. But harmony by itself can be “lipstick on a pig”

Key?  I actually believe that the musical key and harmonic alignment, is key.  That the fundamental  resonance of a piece of music is what “moves” us.  A good example of this are the various recordings of I’m In The Mood, by John Lee Hooker (look it up on Spotify or YouTube).  The recordings in the key of G minor sound kind of Country and wild.  The recordings in E or E-flat are heavy – like the most deep, dark passion – like it really is the mood for love.

A related personal experience: in 2008, I was rehearsing with my band (the Cosmic Marvels).  The singer had written a new song in the key of B-minor.  Both the drummer and I had such a strong, visceral reaction against it that we both rebelled and refused to play it.  As our drummer later related, it was as if “every fiber of my being was reacting against the song”.  Perhaps it was too harsh, but we parted company with that singer the following week.

Similarly in 2015 – and forgetting the prior experience – I was in another band, The Moonbeeems – when I asked the band if we could try one of our songs in the key of B-minor.  When we had finished the song one of our singers  was so physically upset that she stormed out.  Now, it could have been my manner or a misunderstanding, or a coincidence, but, again – it was the key of B-minor.  And, that was basically the end of that band too.

So clearly – B minor: not a great key for band harmony!

But what is the “right” key – or right keys?  For me, the challenge is to find those vibrational frequencies that really do connect our essential being, and to construct a musical vocabulary that can be called on by musicians in the same way that poets have words with specific meaning that they combine into various rhythms and rhymes to convey “truth” and beauty.

But which vibrations shall we pick?

Unfortunately, Western culture and musical theory have left us in a shambles:

1. The A-note is the modern reference pitch – but the evidence is that in ancient times, it was not A

2. The vibrational frequency of that A reference pitch has been altered from its standard of 432 vibrations per second (Hertz, or Hz) documented in the 19th and 16th centuries and before, to 440 Hz made a standard in 1939.

3. Western musical instruments are tuned to “Equal Temperament” – which approximates all notes of the 12-note harmonic scale except the octave – so that even when your piano or guitar is in tune to A, it’s out of tune with its own harmonics!

4. Modern music seems to attach no significance to Key – so key seems to be chosen based on convenience, rather than mood or intent

To summarize: we don’t know what keys to play in; we don’t know what note should be the foundation of that key; we don’t know what frequency that note should be at; and anything we play on a piano, guitar or other fixed scale instruments isn’t even in tune with itself!

Occasionally though, we will still hear a piece of music which from its first note immediately grabs us.  Whether by fluke or inspiration, the artist had recorded the song in a certain key, with a certain “out-of-tune” instrument – or with a vibrato which somehow transcends the mechanics of making music and connects with our soul.  There is this moment of immediate resonance within us – at a deep, personal level.  Our thirst for the sacred kicks in and we rush out to hear this “gem of enlightenment” over and over.

Unfortunately, with modern electronic keyboards, and electronic tuning devices based on equal temperament, musical “happy accidents” are fewer and further between.  Jimi Hendrix is no longer spending hours tuning his guitar until it feels right – or pulling the be-jesus out of his whammy bar to hit the right sounds.  The old piano at Dynamic Studios in Jamaica has been replaced by electronic keyboards that play exactly according to the broken Western conceptions of what musical notes should be.  We are locked into 440 Hz and Equal Temperament.  And now, through the “miracle” of “Auto-Tune”, our human voices – the most essentially emotive component of music – are being altered in recordings and live performances to align with the Equal Temperament keyboard instead of aligning the keyboard to the natural harmonics of the human voice – (which, by the way, is entirely possible to do with the more sophisticated modern keyboards).  Add to this, the harmonic-stealing medium of “digital” and the increasing scarcity of live music, and we’re in a pretty sorry state.

DJs? – sure, gotta love ’em.  But re-assembling music recorded in equal temperament and 440 Hz, with no real understanding of key just leaves us parked somewhere between the 1960 and 1980s – forever sampling and repeating the same sorry dance.  And meanwhile, all of this harmonic deficiency is covered up with hyper-bass until all we can do is drink ourselves into oblivion to make it sound alright.  No wonder people stay home and watch the TV – and what do they see?  A world increasingly destroyed by our own dis-harmony and lack of sympathy and insight.

Even our options are wearing thin.  Digital recordings of “primitive” music from India, or Ireland or the Amazon or Indonesia – digitally recorded and then compressed for quick streaming download, and, if recorded in a studio – probably re-calibrated to A = 440 Hz, Equal Temperament.

So, where is the music that can penetrate our daily dross and re-connect us to our cosmic vibratory dance?

EVIDENCE OF FUNDAMENTAL NATURAL VIBRATION

Well, let’s start with the cosmos then.  NASA tells us that the vibration detected from black-holes in deep space (and time) resonates at a B-flat, 57 octaves below what we can hear.

Now, if that was it, our quest might be over.  But there’s lot of incompatible and contradictory information out there – e.g. we find discussion of the resonant nature of the Pyramids in Giza (F-sharp – which isn’t part of the B-flat harmonic series, see Appendix); or discussion about the resonance of the Earth as it interacts with its atmosphere (the Schumann resonance, 6.5 Hz to 7.8 Hz – well, which is it?), or Solfeggio frequencies, etc. It’s  difficult to build a coherent picture of our fundamental musical vibrations from all this conflicting information.  One can also try the path of intuition, but at some point – but how nice would it be to just know what the notes are supposed to be, and get on and play them?!

HARMONIC “STILL POINTS”

Luckily, one evening in a hotel room in Johannesburg, it occurred to me to play some very low, sub-audible frequencies on a tone generator app on my iPhone – just to see what they sounded like through the Bluetooth headphones given to me by my sister for Christmas.

While wheeling through the frequencies at around 6 vibrations-per-second (6 Hz) I noticed a “beating”.  Now, 6 Hz is not a “note” – it’s basically a very fast rhythm.  Imagine a drummer hitting a drum 6 times per second.  But, what was remarkable was not the rhythm of 6 beats per second, but instead a “swooshing” or “beating” sound – like a steam-train – that repeated about once per second.

Players of stringed instrument are familiar with the “beating” sound when tuning a note on one string to match the same note played on another string:  There is a rhythmic oscillation that occurs at the “difference frequency” between the two notes:  If the two notes are 1 Hz apart, the “beating” oscillation will be once per second.  The musician will tune the string until the “beating stops” [masochism joke here] – that’s when the two notes are identical, and are in-tune.  You can hear Joe Walsh demonstrating this at 3:14 here.

But my tone-generator wasn’t generating two frequencies – it was generating one.  So, if I was hearing a “beating”, swooshing oscillation at these low frequencies, the tone-generator would have to be interacting with some other, ultra-low “background” frequency in my environment.  So, what was the other “ghost” frequency that it was beating against?

As I slowly modified the frequency towards 5.4 Hz, the beating slowed to a stop.  Interestingly, 5.4 Hz is exactly the note F – (see Calibrating the Tuner, in Appendix).

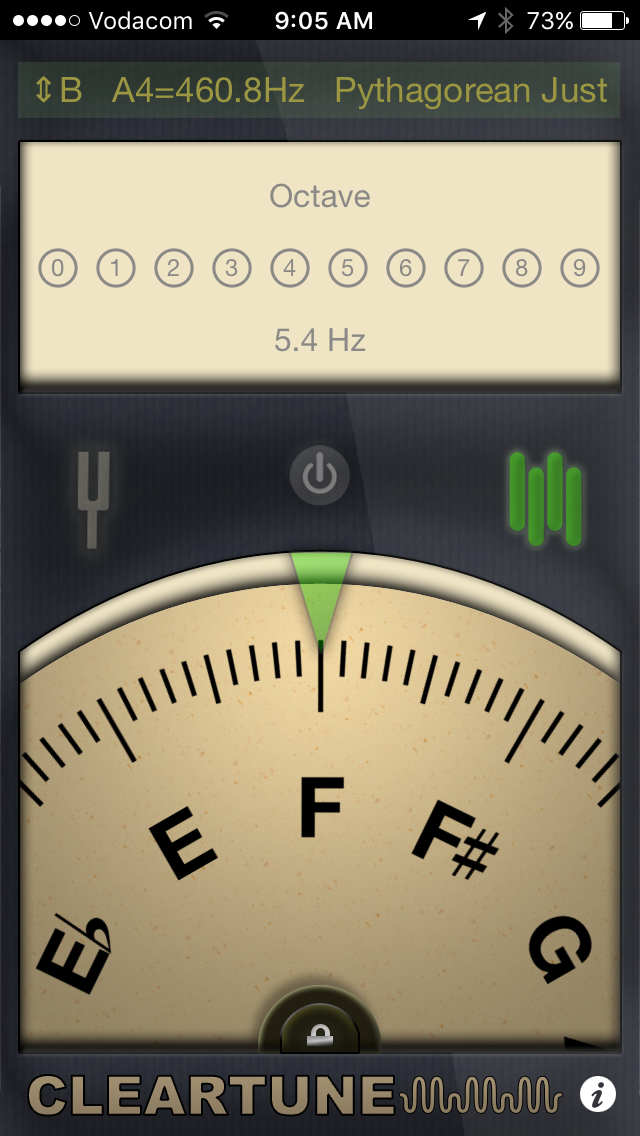
Curious, I turned the wheel away from 5.4 Hz.  And the rate of beating/swooshing increased.  Then as the frequency approached 7 Hz the rate of beating slowed again.  So, I’m speeding up the frequency of the “note” but the swooshing noise is slowing.  At 7.2 Hz, the beating again slows to a stop.  7.2 Hz is exactly a B-flat on my tuner, calibrated as described in the appendix.  And the two frequencies 5.4 (above) and 7.2 Hz (an F and a B-flat) are exactly a musical fifth interval apart (in a 3/2 ratio).

“Curiouser and curiouser”, I thought.  One note creating interference patterns with some unheard vibration is one thing.  Two, musically related frequencies having the same effect confirms the harmonic and musical nature of what I was experiencing.  These two harmonically related frequencies – 5.4 and 7.2 Hz – were vibrating against some other “background” tone, that I couldn’t hear.

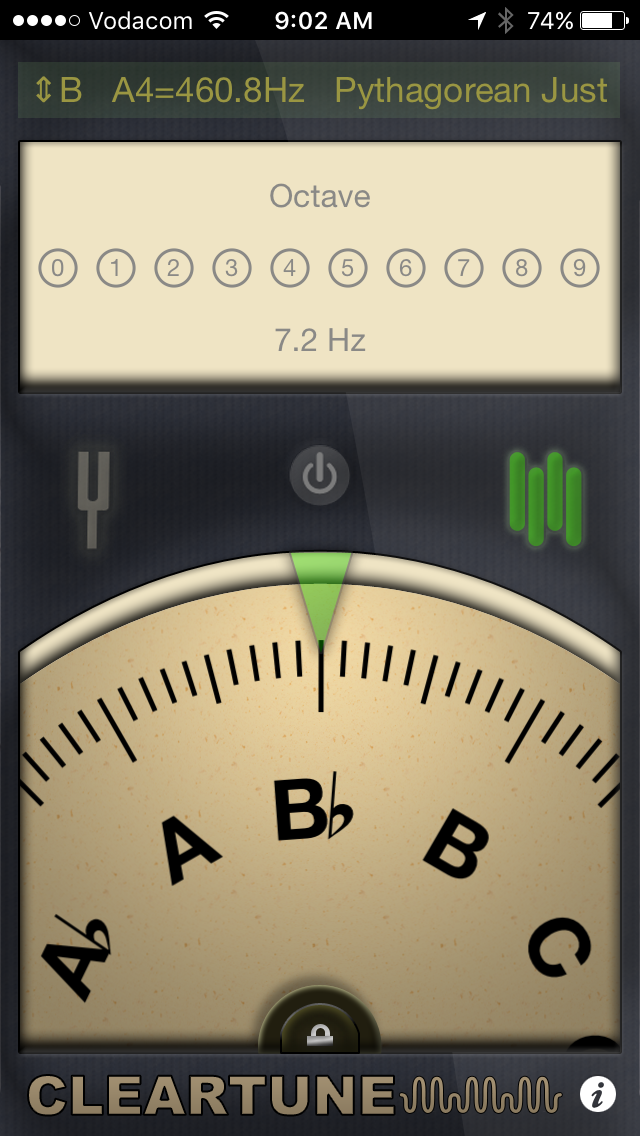
Moving the dial on, the same occurred at 10.8 Hz – double the frequency of 5.4 Hz, an octave of the first F.

So, we have a sort of Pythagorean resonance occurring at three frequencies (5.4 Hz, 7.2 Hz and 10.8 Hz), a musical fifth and an octave – vibrating in consonance with some hidden, sub-audible frequency.

But, where was the second vibration coming from – the cause of the interference pattern and the “beating”?

· From something in the room?  The fridge?  I tried it out on the balcony – same effect.  And I’ve tried it in England and the US – same thing

· From the tone-generator itself?  I re-calibrated it to 440 Hz and equal temperament, to see if that was a factor.  Same thing

· Was it an artifact of Bluetooth itself?  The carrier wave of Bluetooth is standardized at 2.5 GHz – which corresponds to a frequency of 4.47 Hz, not 5.4 Hz.  So that doesn’t seem to be a factor.

Or is that the B-flat frequency, (and its F/fifth counterpart), are a part of the fabric of our universe – as NASA’s recordings of black-holes indicate?  A sort of unheard, background vibration.  Basically, that’s what I reckon – overtones of the underlying fundamental vibration of our universe are creating an interference pattern with the sub-audio vibrations from my tone-generator.

OTHER EVIDENCE OF B-FLAT AND F AS FOUNDATIONAL RESONANCES

Regardless, all this could be a fluke, or the artifact of some interference in the technology.  So I looked to see if these frequencies showed up elsewhere.

SPIRITUAL NUMBERS

I shared my findings with my friend, Susan Alexjander – who has done importand and inspirational research in this area, including measuring the resonant infrared frequencies returned by DNA – and has created her own music based on this, (and a wonderful piece which coincidentally combines the resonance of a black hole with a pulsar).  Her response was immediate, “54, 72, 108 – these are sacred numbers!”  I had not noticed this – but indeed, 5.4 Hz, 7.2 Hz, 10.8 Hz – if you remove the decimal places – are sacred numbers mentioned in ancient Hindu texts and elsewhere in Numerology.  Another interesting coincidence.

ANCIENT INSTRUMENTS

I then Googled ancient musical instruments that don’t change over time such as bells, horns and flutes.  I found these cast bronze bells exhumed from ancient China:

Raising the F vibration (10.8 Hz) by a few octaves (multiply by 2 a few times) to 345.6 Hz – we now have a frequency within the range of normal music.  It’s still an F – it’s just an F we can make music with.  As it turns out, these three-thousand year old Chinese bells are based on a central tone of 345 Hz – our “F”.

As were these flutes from ancient Egypt:

Along the top of the chart above, I’ve put the frequencies of a harmonic scale based on the B-flat (7.2 Hz) and F (5.4 and 10.8 Hz) frequencies I discovered.  The four rows below this are the measured frequencies from each of the four flutes.  And I’ve highlighted in red those flute frequencies that closely match the expected frequencies of a harmonic series based on our B-flat, 7.2 Hz fundamental frequency.  That’s pretty close matches, across the four flutes, for F, G, B-flat, C and G-sharp – and all notes within a harmonic scale based on B-flat.

Just the fact that the first note of the first flute is just 0.1 Hz from our 345.6 Hz “discovered” frequency for F is pretty amazing.  It suggests that this flute maker knew this frequency, strove to match it in his/her flute making, and had a pretty amazing means for checking the instrument’s alignment with this frequency – presumably not a digital tuner!

The audible difference between 345 Hz and 346 Hz for example, is barely perceptible consciously – and yet this ancient flute-maker matched that tone not by 1 vibration per second, but by 0.1 vibrations per second!  The other flute is still only 2 Hz off, at 343 Hz.

And if we raise 345.6 by another octave to 691.2 Hz, we see that this note is also very closely approximated as the “high” F, in the other two flutes.

Also, three of the flutes are extremely closely aligned to each other on the B-flat note – indicating it was considered to be very important to get this note correct – perhaps there was a reference pitch for this note which they used when making these flutes.  And we see similar close matching across flutes at the notes, G, G-sharp, C – all essential notes of the B-flat harmonic series.

· The fact that the F note is the fundamental note on two of the four flutes indicates that the Egyptians felt F to be fundamental, not A.  And in fact, of the four flutes, only one has even a remote approximation of the note A

· And also, in all four flutes – from different times and places in ancient Egypt – the F frequency is in close proximity to the “still point” frequency I found on my tone-generator.

CYMATICS

Meanwhile, Cymatics is a fascinating study showing how matter (lycopodium powder or salt, usually) resonates to create different geometries at different frequencies of vibration of a flat surface – or dish of liquid.  It turns out, the first frequency that creates a shape in this video is 345 Hz – our F note!

As the chart below indicates, the video shows many points where interesting, geometrical shapes form, corresponding to frequencies in the harmonic series derived from our F and B-flat “still point” frequencies.  (I do realize there’s some “drift” here as the frequencies rise – but the accuracy is still around 99%, e.g. 2041/2073.6 – and I’m not an expert on any “lag” that the vibrating substrate might have with these kinds of cymatics – or whether they guys running this experiment turned the gauge onwards a little after the frequency that generated the shapes was reached.):

But the first two frequencies at least are almost exact matches to the harmonic frequencies based on the two frequencies I had discovered on my tone generator.  Perhaps the universal resonance of B-flat detected by NASA (and its perfect 5th harmonic, the F note) does indeed imbue our daily lives with a resonance which inter-plays with every vibration and sound we feel and hear  – and this was also known to the ancients, somehow.

THE MUSIC OF THE SPHERES

In Jacob Bronowski’s TV series,  The Ascent of Man – episode 4, “Music of the Spheres”, Bronowski demonstrates the physics of musical harmony advanced by Pythagoras and his disciples on the Greek island of Samos; showing how a stretched, vibrating string will yield different musical harmonics of the original vibration when touched at various whole-number divisions along its length.

When I watched this, aged 17, as a guitar player I already knew the interesting effect of “playing harmonics” – just touching the little finger to the string, right above the 12^th fret, without even pressing down – to yield a singing, pure tone, one octave above the note of the original string; going from a low D to a higher D, for example.

Some say Pythagoras learned this from his time in Egypt – that touching a vibrating string at whole integer divisions of its length creates still nodes – equi-distant along the length of the string – like “mini” “strings within the string” – resonating at harmonic overtones of that fundamental tone.  In other words, the building blocks of melody are all encompassed in each fundamental string.  You don’t just get the octave, you also get the musical 5th interval, the major 3rd, the 7th and the 9th harmonics, depending on where along the string’s length you touch with your finger.  Every string is a little symphony all by itself.

So, maybe there’s a “string” – like the “monochord” of yore –  from which all the harmonics of universal energy emanate.

THE HARMONIC SERIES

One Monday morning in early 1994 – being between jobs – I went to the trouble of playing harmonics at measured distances along the guitar string, and figuring out what note was generated where.

· Touching the string at the mid-point gives us an octave because the string is now vibrating in two parts, each at twice the original rate.

· Playing a harmonic, one third of the distance along the string creates two “still point” nodes – three equal divisions of the string – all vibrating at three times the rate of the original, to provide what is called the “fifth” in music (because it actually takes 5 notes up the scale to go from the first note to this note)

· Touching the string a quarter of the way along its length generates another octave

· At a 5th of the length of the string, the musical third will be generated

· etc.

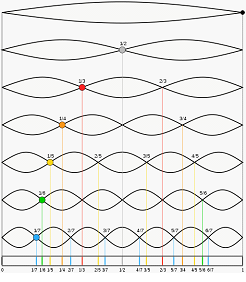
Image Source: https://en.wikipedia.org/wiki/Harmonic

Here are all the harmonic notes  – generated by playing harmonics on a B-flat string – starting 1/2 way along the string, going to a 9th division of the string:

And, in sequence:

The harmonics described above are all “over-tones” – vibrating faster than the original note.  As players of stringed instrument know, the easiest harmonics to play are:

1. Octaves (at a point half-way, or a quarter way, down the length of the string)

2. Fifths (at a point a third of the way down the string)

3. Thirds (a fifth of the way along the string).

4. “Seventh” harmonics (played at one 7th the string length) are more difficult to play – and after that it becomes difficult to get the harmonic to ring at all. They’re just not so prevalent in the fundamental note.  (Unless you’re Eddie Van Halen with a Marshall stack playing micro-harmonics).

Modern “fast Fourier” spectral analysis of sound bears this out – that the more esoteric harmonics are fainter and less resonant.  Here’s a diagram of the relative amplitude of harmonics generated by a violin:

· Four Octaves of the fundamental note (G)

· Two Fifths (D)

· One Major 3rd (B) harmonic

· One 7^th (F)

· And some un-marked notes which appear to be another Major 3rd (B), another fifth (D), another Octave (G) and an 11th harmonic (C-sharp), plus some micro-tonics

… all resonating from within the one string being played – the G.  And the relative loudness of these harmonics is in fact what differentiates the sound of a saxophone, for example, from a trumpet or a violin:

[Image source: University of New South Wales Physics Department]

THE ROLLING STONES!

What’s this bunch of reprobates doing in our voyage to the center of music?

It turns out that the 5-string “open-G” tuning taught to Stones guitarist Keith Richards by Ry Cooder in 1968 exactly follows the harmonic series.  In bold are the harmonics to which open 5-string guitar is tuned:

1. Octave

2. Octave

3. Fifth

4. Octave

5. Major Third

6. Fifth

7. Seventh

8. Octave

9. Ninth

It’s as though the five strings are tuned intentionally to ring out the natural harmonics that are present within the first string.  5 strings resonating as one:

1. G (fundamental)

2. D (fifth)

3. G (octave)

4. B (major third)

5. D (octave of fifth)

With the use of a capo placed across any fret you like, the fundamental note and the resonance of the entire instrument can be changed easily – to suit the inspiration of the song, while retaining the harmonic relationship between the strings – and then fretting and playing specific notes allows the inherent harmony of the vibration to be explored as rhythm and melody.

Brown Sugar, Tumbling Dice, Start Me Up – many of the hits from 1968 to the present day were written and recorded in this tuning.

Prior to that, Keith had also used 6-string open-D, open-E and open-E-flat tunings – used on such late-60s songs as Street Fighting Man, Jumpin’ Jack Flash and You Can’t Always Get What You Want – and also used by Elmore James and some of the blues and slide-guitar greats.

Keith Richards himself remarked in notes at the Exhibitionism exhibit that he is fascinated with “how one string makes another vibrate” – called sympathetic vibration.

This very insight opened up a realm of possibilities for me – in terms of playing chords while playing notes that are harmonically aligned to the fundamental resonance of the open notes.  This is the fundamental nature of music.  And, if we could find the right chords,  perhaps, this could be the fundamental music of nature!  

Keith himself has remarked that open-tuning is like a sitar – with a sort of drone note ringing in the background.  The enduring popularity of the Rolling Stones’ music, when Keith (and Mick!) have constructed songs around this approach, shows that these open tunings and the way of playing them, really “strikes a chord” with many people.

THE “MODES”

You get a different emotional feeling in a piece of music depending on which note of the scale it starts on – which, by the way, is usually the one it ends on – that’s how you know you’re back to the song’s point of rest – its “point of view”.

And the reason that certain music sounds happy or sad has to do with which note of the harmonic series that starting note is.  Depending on whether you start your piece of music on the first harmonic, the second harmonic, the fifth harmonic, etc – you get a very different feeling in the music.

If you have a piano handy, try playing only the white notes:

· Starting at a C – you get a nice, jolly, major scale – found in many Christmas carols

· Now, play the same white notes starting at an A – gives you a maudlin minor scale

Same notes – different starting note – different feeling.

This is not just because certain notes carry an emotional weight (although I believe they do) – but because the intervals – the gaps between the notes as you climb the scale from your starting note – are spaced differently depending on the starting point.

If you start a melody on the second note of the harmonic series (the A-note, if you’re still playing white notes on the piano), it forces the third note in the scale to be just a semitone above the second note – and that’s where the sound we recognize as sad comes from.  It seems to be a common, psycho-acoustic reaction across all cultures.  A scale that starts with the second note of the harmonic series is known as a “Minor” scale (or Aeolian mode).

If you start with the fourth harmonic (the C in our white-note example, above), you get a more optimistic, “major” mode.  The interval between the second and third note is a whole tone, instead of a semi-tone.  And the interval between the 7^th and octave is a semi-tone – it too has a wider step.  It sounds happy, complete, robust, confident, healthy – if a little proud.  This is the “Major” (or Ionian) mode.

There is a mode name for each of the seven starting positions in the harmonic series.  For example:

· If you start with the first note of the harmonic series, it’s called Mixolydian mode.   It sounds happy (major third), though a little poignant (minor 7^th).  But, being as this mixolydian “mode” is actually the natural harmonic series itself, the music played in this mode matches the “personality” of the universe itself, in my view: “happy” yet “poignant”

· Aeolian mode, (the familiar western “Minor” key – just doesn’t have the energy for a full major third, it also has a minor seventh.  It has humility (minor 7^th) but generally lacks “get-up-and-go”.  After a while, it’s quite exhausting, like a friend who comes over and moans about their life for a few hours.  It’s a relief when it’s over

· Major (Ionian mode) sounds pompous and over-blown after a while.  One needs a little humility (a minor 7^th, perhaps) as the antidote.

· Phrygian mode starts at the 6^th note of the harmonic series – it is the basis for Flamenco – full of fire and passion, but ultimately, tragic.  It has a minor third, a minor sixth, a minor 7^th.  Everything is “minored out”.

But Western “classical” music, for whatever reason, only talks about Major (Ionian) and Minor (Aeolian).  You don’t see a piece by Beethoven in G-Phrygian – even though it may be – it will likely be called “G-minor”.  And you’re more likely to see a piece in Ab-Major than you are in Ab-Lydian – even though that may really be what’s going on.  Our culture tends to simplify and obfuscate.

Mixolydian mode is generally found in folk and country music.  Because it is the only mode that reflects the natural harmonic series by including a major-third and a minor, “dominant” 7^th – Mixolydian mode is the “natural” mode which describes the harmonics emanating from its fundamental note – so it is the mode we will be looking to to reflect the harmonics of our fundamental, universal tone.

WESTERN MUSIC GOES OFF TRACK

This is the point at which western musical theory tends to get complicated – unnecessarily so, in my view.

The harmonic series (first, second, major-third, 5^th, flattened 7^th, octave) excludes two necessary intervals for western (diatonic) music: the fourth, and the sixth.  They cannot typically be found by playing a harmonic somewhere along the length of a string.

· The fourth harmonic of the western diatonic scale, is really an “under-tone”.  It is the note below our fundamental note whose “fifth” harmonic made our fundamental note.  It’s as though there’s a string, three times longer than ours, whose fifth harmonic (played 1/3 along its length) yields our fundamental tone.  But, if there is truly a universal “drone” frequency that underlies all, then at some point there is no lower harmonic – we would be playing that fundamental vibration, itself – which the evidence presented here suggests is some octave of a B-flat.

· The sixth note of the western diatonic scale (e.g. G in a B-flat scale), occurs harmonically as the 9th of the 5th (i.e. F is a fifth of our B-flat fundamental frequency – and G is a ninth harmonic of F).

It’s only when we derive the harmonic series for F that we get all the notes we need for the B-flat diatonic scale.  It’s as though B-flat and F resonate like a DNA spiral – only together giving us the complete tool-kit. (remember – it was B-flat and F – an exact musical fifth apart –  that I detected as “still point” frequencies on my tone-generator)

Most music theory calculates the sixth harmonic, as:

· The 5^th of the 5^th of the 5^th of the fundamental. For example, G is the fifth harmonic of C, which is a fifth of F, which is a fifth of our B-flat starting-point.

· (e.g. 460.8 for a B-flat) x 3 x 3 x 3 = 388.8 Hz (when you bring the octave back down)

· Or the sixth can be determined as the 3^rd harmonic of the 4^th harmonic. e.g. D-sharp/E-flat is the 4^th of B-flat, and G is the 3^rd harmonic of D-sharp

· e.g. (460.8 / 3) x 5= 384 Hz

Note that these two approaches yield two different frequencies for G – i.e. 388.8 Hz and 384 Hz.  Interestingly, as you’ll see in the section on “constructing a naturally harmonic musical foundation”, my tuner says G should be 384 Hz, and my harmonic construction says it should be 388.8 Hz, based on the 9th harmonic of F .  So, there are inherent micro-tones in music which western music ignores – we are supposed to pick one.

The good news is that there are guitar builders, like Jon Catler, who recognize this and let us have both.  However, for simplicity, I’m choosing the one most closely resonant to B-flat and F, which is 388.8 Hz, as my G frequency.

THE “CYCLE OF FIFTHS”

I was fortunate to have had a digital, sub-audio tone generator, but in the 2,5000 years since Pythagoras left us the ancient knowledge on which bells and flutes were constructed has been lost.  So, we can’t blame our forbears for making mistakes – one of which, in my opinion, being the idea that music should be playable in any key.  It’s like saying, we’ve forgotten the ingredients for making meringues, so just whisk anything up and pop it in the oven.  Bon apetit!

Most music theorists have  held the position that Pythagoras constructed the musical scale by calculating fifths of fifths of fifths etc. until he’d derived all 12 notes of the diatonic scale.  But to me, considering how easy it is to play the 2nd, 3rd, 5th and 7th harmonics on a single string – and how faint the “harmonic of a harmonic” is to hear – I don’t see why he would veer off into a theoretical approach when he had the mechanics for generating all 7 notes of the musical scale at his fingertips – literally – by touching his finger at various geometrical points along the length of a two strings tuned a harmonic fifth apart.

Nonetheless, Western music has adopted the fifths-based approach, rather than the practical approach – and thereby unearthing a practical problem for itself, called the Lemma, or wolf-tone.

LEMMA TELL YOU A STORY

If you start with a basic frequency and multiply it by 3/2 you generate a musical fifth (e.g. B-flat to F) and if you repeat that multiplication by 3/2, 11 times you will make a complete round of the “cycle Of fifths” bringing you back to your starting note and yielding all 12 notes of the western chromatic scale (as illustrated below).  But, in reality, the note you end up with is not exactly the note you started with.

For example, let’s start the cycle with a B-flat frequency of 460.8 Hz.  460.8 x 3/2 (a fifth harmonic – our F of 691.2 Hz).  And from there, if we multiply this by 11, it should take us step-by-step around the cycle-of-fifths 11 more times to bring us back to a B-flat. But what frequency do we actually end up with?

691.2 Hz x 11 = 7,603.2 Hz.  Divide that by 16 to bring it down 4 octaves and it’s 475.2 Hz,  not the 460.8 Hz we started with.  And that little gap – the “lemma” – isn’t a whole note, it’s just a little chunk of dissonance – or so they thought.

So, harpsichord, piano and organ makers, tuners and composers, including Bach and Mozart, tried to account for the lemma by various schemes of “temperament” in which that gap was apportioned across the 12 intervals of the western diatonic scale – in such a way that the popular keys would suffer the least from the averaging, and the less played keys would suffer the most.  Some of these “temperaments” are pleasant, ensuring perfectly resonant 3rd harmonics in one or two keys – and certain pieces of music were written specifically for these temperaments.  In fact, Bach’s “Well Tempered Clavinet” was a series of explorations of multiple different temperaments.

Eventually, an equal apportioning of the lemma across all the intervals – known as “Equal Temperament” – was accepted as the standard way of tuning fixed pitch instruments (such as piano, organ and guitar) – because it enabled the same piece of music to be played in all keys, with equal harmonic dissonance.  It’s typical of how humanity will force the evidence to fit a theory that rather than look at what the evidence may be telling us is wrong with our theory.  So, they tried to bury the lemma and keep their view of the universe as a simple clockwork mechanism – and wait for a more enlightened age (us) to figure it out.

The averaging that Equal Temperament (ET) introduces breaks the sympathetic vibration across the harmonic series.  The whole self supporting interplay of harmonics is broken.  The music “cancels out” its own harmonics and is essentially dissonant.  Today we have food-like substances in our supermarkets – and we have music-like vibrations available for download – thanks to Equal Temperament.  Welcome to modern times!

But the universe isn’t a watch-works as our 17th century predecessors thought; its more like a harmonic web of vibrating energy.  Quantum mechanics tells us that matter is really an energy wave – photons, electrons, protons and neutrons all spinning and vibrating in harmony with each other.  Imagine if the vibration of these waves “didn’t quite add up” like the cycle of fifths doesn’t.

THE LEMMA IS FRACTAL!

You know what else doesn’t quite add up?  Fractals: the tiniest gap at the end of the fractal ends up being a holographic mirror of your starting point.  Some scientists and authors are investigating the fractal nature of reality.

And here’s a little fractal insight I discovered for myself.  Let’s revisit that example above.  We start with our “still point” frequency of 7.2 Hz.  But that’s too low so we octave it up to 460.8 Hz to give us a B-flat we can hear – and we start the cycle-of-fifths with that frequency.   As above, 460.8 x 3/2 gives us a fifth harmonic (an F of 691.2 Hz).   If we multiply that by 11, it should take us around the cycle of fifths 11 more times to bring us back to B-flat. What frequency do we actually get (once we octave it down a bit)? 475.2 Hz.

So, what’s the size of the Lemma? 475.2 Hz minus 460.8 Hz = 14.4 Hz.  Do you recall that our “still point” vibration for B-flat is 7.2 Hz that’s half of 14.4 Hz – an octave below.  So the gap we encounter between our ending note and our starting note is a small number of vibrations per second which, it turns out, happens to be a sub-octave of the very B-flat note we began with!

So, there is no gap – just a fractal fragment which itself is a harmonic microcosm of the note we started with.  And in turn, that little harmonic fragment will generate its own harmonics – which will produce its own fractal fragment, and so on, and so on…

For some reason, music theorists didn’t examine the size of the gap between the last note of the cycle and the first.  Instead, they felt this was a fundamental flaw in nature – in the “music of the spheres” – and attempted to make it disappear.

So, the Lemma is not some useless, unexplainable gap; the Lemma is a sub-harmonic of our starting frequency.  And thus the cycle of fifths does not negate harmony; it reinforces it and perpetuates it – just as a fractal or a hologram perpetuates itself in the tiniest left over detail which contains the seed of the whole.

Did no-one else notice this before they went off any invented all the different “temperaments” of western music to try and eliminate this gap – including the abomination that is Equal Temperament?  Beats me – the idea came to me at 2 o’clock in the morning in 2017, and it’s pretty simple mathematics to prove it out.

For a more detailed exploration of this, take a look at my “lemma” page, here.

FOUNDATIONS

OK – so musical harmony is fractal – the cycle-of-fifths is like a universal, harmonic fractal-generation engine.  But if matter is vibration – all held in delicate interplay – is their a cosmic “first energy” which sets it all in motion?  The starting frequency for the cycle-of-fifths, as it were?

The good news is, I believe, is that we know what it is – it’s the 7.2 Hz “still point” vibration I stumbled across it with my tone-generator.  It is a B-flat vibration which intersects our sub-audio plane like a ripple of energy, reinforcing vibrations which align to its harmonics and cancelling out those that are en-harmonic.  A wave of natural harmony for us to align ourselves to.

CONSTRUCTING A NATURALLY HARMONIC MUSICAL FOUNDATION

OK,  let’s build a musical scale the right way, from the two fundamental frequencies we discovered for B-flat and F.

(If you get lost here, you can scroll down to the big chart where I summarize all the notes that I find in the small tables, below.)

The first table below investigates the harmonics based on the “still point” vibration of 7.2 Hz (B-flat) that I had discovered on my tone generator.

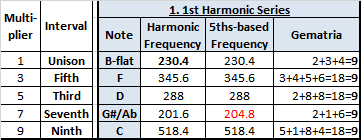
1. Starting with a frequency of 230.4 Hz (several octaves above 7.2 Hz), we treat this frequency of 230.4 Hz as though it is the frequency of a vibrating string, and then divide that string successively by 3, 5, 7, 9 (see the “Multiplier” column) to calculate the harmonic frequencies that we would get by touching the string at these “nodal” points.

2. The second column is the name of the musical interval generated at each of these points – e.g. with the Multiplier of 3 (touching the string at a point 1/3 along it’s length) we generate the musical interval which is called (in a typically confusing manner) “the fifth” – because it is the 5th note when you play do-re-mi-fa-so.

3. The third column is the name of the note that these harmonics correspond to.  Because we started with a B-flat, the “fifth” is an F, the “third” is a D, and so-on

4. The 4th column is the actual frequency which results

5. In the “5^ths-based Frequency” column, I put what my calibrated tuner says is correct for that named note, calibrated as it is, for “Pythagorean Just” intonation – using the interpretation that Pythagoras used the cycle of fifths, as discussed above.  Those items in red, highlight mismatches between the harmonic frequencies we generate (column-4) and the frequencies that western musical theory says are supposed to occur for the starting frequency in question

6. And, I’ve added a “Gematria” column. Gematria, is the concept that by adding the integers of a number, we unearth its common, symbolic significance and harmonic value.  e.g., for the 7.2 Hz number we had found for B-flat: 7+2 = 9.  What is interesting is that EVERY “Harmonic Frequency” we generated in this chart resolves to a 9.  Another point of correlation of these “still-point” frequencies to bodies of knowledge passed down to us through the ages.

OK, so now we understand the structure of the table – let’s look at the data.  Here’s the table again so you don’t have to scroll too much:

Table 1 – harmonics of B-flat

In the second data row (for “Fifths”) we have touched our imaginary finger one third of the way along our imaginary B-flat string.  This multiplies the frequency of the fundamental tone by 3 to give us a fifth.  (230.4 Hz  x  3) = 691.2 Hz.  And, because 691.2 number is a little unwieldy, we go down an octave and, voila, it’s: 691.2 / 2 = 345.6 Hz (F).  Yes, music lovers, we could have just multiplied the frequency by 3/2, but it’s easier for my simple brain to understand it this way.

· We record this generated frequency in the “Harmonic Frequency” column. We repeat this for multipliers, 5, 7 and 9 – recording the resulting frequencies and the notes they correspond to, in the appropriate row.  The result is 4 new notes, harmonically related to the starting frequency, from which we can make chords and melody (B-flat, F, D, G#, C)

In the next table, we explore the harmonic series generated by the strongest harmonic of B-flat – its “fifth”, which is F.  You will recall that F was also the other “still point” frequency we had found with the tone generator.  We’ll borrow the 345.6 Hz for F which we generated in the table above as our starting point – but note that this F an octave of our original “magic” tone of 10.8 Hz (10.8 x 2 = 21.6 x 2 = 43.2 x 2 = 86.4 x 2 = 172.8 x 2 = 345.6 Hz = F:

Table 2 – harmonics of F

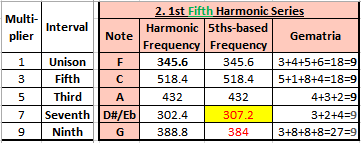
As before, we multiply this frequency by 3, 5, 7 and 9 to generate its harmonic series.  And this yields three new notes:  the Major Third of F (A) – which is the major seventh of B-flat; the Dominant Seventh of F (D-sharp/E-flat) – which is the fourth of B-flat; and the Ninth of F (G) – which is the sixth of B-flat.

Put these together, and we now have all the notes necessary for several scales: B-flat Mixolydian, B-flat Ionian (major), F Dorian, F Mixolydian.  We haven’t traversed the cycle of fifths 11 times, building up lemmas  We’ve simply collected the notes of the harmonic series of the two “still point” tones that we detected (B-flat and F) and constructed scales where every harmonic is exactly – musically and mathematically – resonant with the fundamental, “magic” tones.

We now have all that we need to construct complex, modulating music – harmonically self-reinforcing and aligned with with the background, vibrational noise of our NASA’s black-hole recordings, my experience with nodal still point vibrations on my tone-generator, ancient musical instruments, cymatics and – dare way say it? – gematria.

Originally, I had felt that we should stop with just the harmonic series for B-flat and F – and the eight notes this provides us.  But I since have felt that if we keep going, until we have generated all 11 notes of the Western chromatic scale, that we are building a full palette, circling downwards towards our “sub-lunary sphere” and therefore encompassing some of the more discordant energies that make up our existence on this plane.

So, let’s do that – might as well get the whole palette.   But first, one note:

Note:  It turns out that when you put the Seventh found above(D-sharp/E-flat) into a musical scale with a B-flat, it should be the “fourth” harmonic of B-flat, but it sounds bad.  And to bear this out, if we generate the harmonics from this flavor of E-flat, none of the resulting harmonics resonate with our original B-flat and F frequencies – as shown in table 2b.  This is a problem which Just Intonation luthiers like Jon Catler have taken into account, by including both versions of the 4th harmonic in their guitar necks.

Table 2a – harmonics of Eb (as a dominant 7th of B-flat)

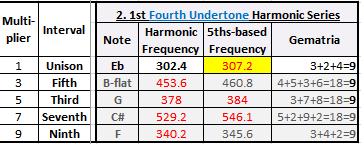
Another way to calculate the fourth is as though there is a string three times longer than our original B-flat string which, if we touch it a third of the way along its length gives us a B-flat.  So, instead of 3/2, it’s 2/3.  2/3 x 460.8 Hz (our B-flat) gives an E-flat/D-sharp of 307.2 Hz (compared to 302.4 Hz).  This “fourth-based” E-flat actually sounds sweeter in a musical scale with B-flat.  So, here are the harmonic frequencies generated from this E-flat.  As you can see, this E-flat does create harmonics of B-flat and F which match our original frequencies.

Table 2b – harmonics of Eb (as B-flat x 2/3)

OK, B-flat was our starting point in the first quadrant; its fifth (and strongest harmonic) – an F – was our starting point for our second quadrant; and the fifth of that F (a C) is the starting point for the third quadrant below (in yellow).

Table 3 – harmonics of C

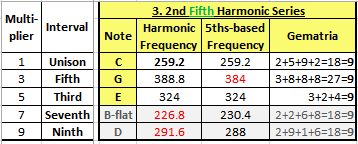
The only new note we get from the “C quadrant” is the musical 3rd – which is an E (which is a tri-tone to B-flat, the “devil’s interval”.

Also note that, in gray, the frequencies for B-flat and the D we generate from a C are slightly different from those generated as harmonics from B-flat in our first quadrant – as highlighted in red.  That “fractal harmonic entropy” which manifests as the lemma is starting to make its presence known.  My solution?  I’m going to stick with the original frequencies for B-flat and D that we had in the first table.  Remember, we don’t want to play in all keys – we want to play in the keys which resonate with our “musical DNA” frequencies for B-flat and F.

Let’s move on to explore the harmonics of our next strongest harmonic, the fifth of C which is a G.  Although, as you can see below in gray, the frequencies we are starting to get no longer match the frequencies we found for these notes in the first three tables.  Fractal entropy is making its presence known even more emphatically – and while these may be valid frequencies if you are capable of playing spacey, micro-tonal music, I’m not.  I’m going to focus on the main harmonic alignment – because I like simple music.

As above, this new table yields just one note we haven’t generated before – the third harmonic, in this case, a B (also the diminished 9th of B-flat).

Table 4a – harmonics of G

Note: Another way to generate a G would be as the third harmonic of the alternate E-flat harmonic we explored in table 2-b, above.  In so doing, we get harmonic equivalence for the D and A frequencies we found earlier – but a contradiction for our frequencies for F and B. Again, some luthiers will support both flavors of the 6th harmonic (G in this case), such as Jon Catler’s FreeNote 24-fret Just Intonation guitar neck.

Table 4b – harmonics of alternate G

The next fifth is a D.  D is also closer at hand to B-flat as the third harmonic of B-flat.  This harmonic series yields one new harmonic note, again the major-third, F-sharp – which is an augmented 5th of B-flat:

Table 5 – harmonics of D

And the strongest harmonic of that D is its 5th, an A which gives us the starting point for table 6 – which yields just one new note (once more the major-third), a C-sharp – which is the minor-3rd of B-flat:

Table 6 – harmonics of A

Note:  “A”, based on its name, might be thought of as the fundamental note of the musical scale but is actually the last table in our analysis – the most tenuous harmonic when B-flat is considered as the starting note.  Perhaps by intention or irony, western labeling of the musical notes throws most students of music down the wrong path.

Anyway, we now have all 11 notes of the western chromatic scale – those closely aligned to B-flat and F, plus the “ugly” notes: E (from harmonic series of C), B (from the harmonic series of G), F-sharp (from D), and C-sharp (from A).

SUMMARY OF FREQUENCIES HARMONICALLY ALIGNED WITH B-FLAT AND F

Put all this together, and we have the exact frequencies in Hertz for an 11-note, chromatic musical scale that is harmonically aligned to our “still point” frequencies of 7.2  Hz for B-flat and 5.4 Hz for F:

Table 7 – summary of the harmonic series based on our discovered frequencies for B-flat and F

Regarding the discordant notes (B, F-sharp, C-sharp).  I would suggest that they should be used only “sparingly” and as grace-notes, because they are harmonically so distant, and discordant with our starting vibrations (B-flat, F).  We shouldn’t use them as the fundamentals of scales themselves, because their harmonic series would all be adrift from the B-flat and F fundamental frequencies.  But life isn’t always butterflies and rainbows, so, when you need a little “venom” in your music, there they are.  However, I submit that what the world needs now is music without venom – and so, generally, I avoid playing them.

UNIVERSALLY HARMONIC KEYS

So, focused on the keys that are most harmonically aligned with B-flat and F, we can construct music on any of the following keys and modes:

· B-flat mixolydian:- is the same notes as:

· C minor

· Eb Major

· F Dorian (blues-like)

· G Phrygian

· G# Lydian

· F is the 5th of Bb and its harmonic series adds an A (as the major third of an F) to the proceedings, and F mixolydian is the same notes as:

· G Minor

· B-flat Major

· C Dorian

· D Phrygian

· Eb Lydian

So, there’s the ability to blend an merge modes from across the two fundamental mixolydian keys of Bb and F.

It’s interesting to note that in the world of entropy, the fundamental principle that sets it all in motion – B-flat – really only exists in one of these tables. It’s the elephant in the room which you don’t really see.

BAR BANDS VERSUS “SERIOUS MUSICALITY”

Western musical theory is so abstract and artificial that you can’t blame most musicians for not knowing it.  It’s based on the cycle of fifths, and then tries to account for the lemma by dividing it out amongst all 11 intervals of the chromatic scale.  It makes no allowance for fundamental, natural resonance and uses the wrong reference note (A instead of the actual B-flat, a semitone below); and with the wrong reference frequency (440 Hz instead of 432 Hz).  So, it’s no wonder that most musicians spend their time playing other people’s music, trying to capture the excitement they received from that piece of music originally – which probably originally escaped the clutches of harmonic death because the guitar was uniquely tuned, or there was a vibrato on the Hammond organ, or for whatever reason.

But, besides the general “inability to swing” amongst bar bands,  there is another key limitation to their musicality, in my view:  Guitar “Concert Tuning” (E, A, D, G, B, E) lends itself to the keys of E, A and B – and so most easy-to-play guitar music is comprised of E, A and B chords.

Most guitar players don’t question why a guitar is tuned this way, or how it came about.  It is, and therefore that’s how they learn to play it, and these are the sounds that come out of it.  But, as we’ve seen, B is discordant with our “magic” key of B-flat, and I prefer not to play it at all, E is a tri-tone to B-flat (the “devil’s interval”) – although jazz people love that stuff.  So, if there really is a subliminal B-flat resonance in the background at all times, a good portion of the notes coming from a concert-tuned guitar are going to be dissonant with it.

Solution: slap a capo on your guitar on the first fret to put it into F – and every open string is now a “non-ugly” note from our collection.

Pianists have a more even playing ground.  There is no “prejudice” to the instrument – if you’re not playing all white keys or all black keys – it’s pretty much the same level of difficulty no matter what key you’re in.  So, pianists tend to choose keys more on their aesthetic effect, rather than their playability.  This may explain why much piano music is not in E, A or B, but in B-flat, E-flat, G-minor, etc. – keys in sympathy with our magic keys.

In my view this is the fundamental difference between “bar bands” and “serious musicians”.  Serious musicians have in their midst a keyboard player, who introduces more interesting and pleasant keys.  Bar-bands are mostly driven by the guitar player.  It sounds rough – better have a beer!

Chuck Berry! – I hear you cry.  But the unsung hero of those hits was Johnny Johnson – the piano player and original band leader.  And there is a prevalence of B-flat and E-flat in those songs.

Jimi Hendrix! – I hear you cry, but after the initial pyrotechnics with the guitar tuned to concert E, he tuned down to E-flat – for songs such as The Wind Cries Mary – and all of his deeper, more numinous hits.  Hendrix transcended the guitar-driven genre – taking his music to realms of consciousness that have rarely been seen, before or since.  But he had re-tuned his instrument in order to do that.

And, in his way, so did Eddie Van Halen (also in E-flat), and of course Jimmy Page – with DADGAD and other unconventional tunings.

In the Beatles, Paul McCartney tended to write songs in B-flat, F and C because, as a bass-player, he was less limited by the tuning of the instrument – one note at a time, from across the fret-board.  He once taught a friend of mine the B-flat major chord, because as he said, “all the best songs are in B-flat.”  Whereas John Lennon, as a guitarist, tended to write songs with E, A and B in them – and, somehow, we judge John’s songs as musically more limited than the songs written by Paul McCartney and George Harrison.

Another interesting thing about the Beatles is that they became quite interested in the frequency 444 Hz – and used this as their reference pitch for tuning instead of the “destructive” 440 Hz, and the 432 Hz of our tuning – (although, we know better that the reference note should be B-flat and not A, anyway.)  I don’t know where they got that idea, but interestingly enough, 444 Hz is the difference note created by 4 out of 15 of the possible Solfeggio “difference” combinations!  (see my investigation of the Solfeggio “difference notes” here.)  And props to John Lennon for going to the trouble of tuning his grand piano according to 444 Hz for Imagine – which is a great song – even though I don’t think 444 Hz is “essential” 

By the way, I secretly had my baby-grand piano tuned to according to 432 Hz a few years ago.  It was still equal temperament, but when my daughter, who is quite an accomplished player, played on it she enthused how it was more than just in-tune, somehow the dynamics were better: the loud was louder and the quiet, quieter.  I didn’t let her know until later that it was tuned to 432 Hz.

POWERFUL SONGS IN THE “MAGIC KEYS”

Music is a subjective thing.  We like what we like.  In the end, no-one cares about the science – so long as the music moves us.  So, I started a little experiment where I found some of the most iconic pieces of music that I’ve grown up with – the ones which have really moved me – and examined them to see if they are in the “magic keys” that the aforementioned study brought me to.

I’ve started to build a public playlist (which you can check out on Spotify) of these songs in the Magic Keys, as I came across them.  The list is just scratching the surface, but I add to it as I get around to it.

First up, Your Song, by Elton John.  For me, it was always this incredibly poignant love song that underlined the feelings I had for a girl at school when I was 9 years old.  Lo-and-behold, all the notes of the song fall within our magic keys – without any of the “ugly” ones.

Interestingly, Getting in Tune by the Who, a song which starts with the lyric, “I’m singing this note ‘cos it fits in well with the way I’m feeling” is, in fact, in the magic key – at least until the very end when they fancy it up a bit.

One interesting exception is Jumpin’ Jack Flash, by the Rolling Stones.  For me, it’s one of the most powerful, exhilarating riffs and songs out there, but it’s in B.  Our “no-no” key because it is one semi-tone away from our starting note of B-flat, and therefore most harmonically contradictory to it.  Well, it turns out, now that the bootleg of the original recording is available, that it was originally recorded in C, using only our “magic” notes – and seems to have been slowed down in post-production to a B – perhaps to make Jagger’s voice sound more manly (humour).  The way the song was recorded is interesting because it started with Keith Richards playing acoustic guitar into an early Philips cassette recorder, over-driving the internal microphone and gain stage on the recorder to achieve a form of distortion combining the crispness and harmonic depth of an acoustic guitar with the harmonic rounding that occurs when a signal is over-driven through an analog gain stage.  This acoustic guitar track was then played back through the studio monitors, or headphones, and Charlie Watts added the drum track on top of the guitar track – which of course is backwards to how it is usually done.  So, the evidence is that the song was recorded once in C, and therefore encapsulates with it all the universal harmonic content that goes with the “magic keys” – and that this entire encapsulation was then slowed down to a B in post-production, for release.  It retains its original harmonic resonance, but it’s given to us as a sort of slowed-down, microscopic examination of that harmony.  Very trippy.

It’s a Long Way to the Top by AC/DC is in the key of B-flat, but includes C#, which I personally regard as being outside the magic keys.  But there is a power there because it drones, (with the bagpipes, no less!) on that B-flat note.  I will add, based on my section on Synesthesia, where I characterize C-sharp as being “over-reaching”, for a song that is about musical ambition, this C-sharp seems to be exactly the right note for that sentiment.  I’ve always loved the bagpipes, and B-flat is the note that the instrument naturally drones in.  It’s always fun when aesthetics meets science and they agree.

If you’re a Kyuss fan, you’ll be pleased to know that almost their entire catalog is played in C-Dorian mode – within our magic keys.  Something about playing out in the desert with an electrical generator, the peyote and the stars to inspire you, perhaps!

TRUTH HIDING IN PLAIN SIGHT

So, there we were, trawling the depths of ancient history for flutes and bells that might be tuned to our “magic keys” of B-flat mixolydian and F mixolydian – and it turns out that just about every modern horn or brass instrument is built with these keys as its fundamental resonance:

· Most modern flutes are in B-flat – plus C and G.  All keys aligned with B-flat and F.

· A quick check on Wikipedia reveals that the modern Trumpet is also in Bb.  Also, the Cornet, Baritone Horn, Flugel Horn, Euphonium.

· Tubas and saxophones are in Bb, F, C or Eb – all three of the “magic” myxolydian keys – and Eb is mostly an extension of that.

· French horns are F or Bb.

· The Mellophone (whatever that is) is in F.

(Although the point at which these horns intersect with the A note is designed to be A=440 Hz in modern instruments.  You can counter this by pulling the mouth-piece out a little so that A=432Hz, and B-flat=460.8 Hz).

CONCLUSIONS

So, my thought process was this:

Through luck, I discovered two “fundamental” notes that seem to be “the still point of the turning World” – to quote T.S. Eliot.  These two vibrations at the sub-audio level of 5.4 and 7.2 Hz seem to be in unison with some unacknowledged, hidden frequency that creates a “beating” interference pattern with frequencies on either side of these vibrations.

So, we assume that these frequencies are “in tune” with a fundamental, universal vibration, and we generate the harmonic series from these two notes.

So, like strands of DNA, spiraling harmonically through time and space, we have two basic tones (7.2 Hz and 5.4 Hz), creating harmonic content as they go – and providing us a rich palette to draw from for any style of music – from jazz to modal folk music – while staying in harmony with the empirical universal resonance of the B-flat and F tones.  This, to me, is a good foundation on which to build musical compositions!

Reinforcing my personal experience of 5.4, 7.2 and 10.8 Hz being foundational, resonant still points, we have found:

· NASA’s detection of a B-flat resonance across the universe

· Appearance of the numbers 54, 108 and 72 as ancient sacred numbers

· Ancient musical instruments (bells and flutes) constructed around these frequencies

· Bees beating their wings at 230 times a second (our B-flat in that octave is 230.4 Hz – the bee is slightly flat, ha ha!)

· That calibrating my tuner so that B-flat = 460.8 also makes A = 432, which is considered by many to be the correct frequency for A (as opposed to 440 Hz, the current “impostor”!)

· That every tone in our “magic” harmonic scale has a Gematria value of 9 (considered the sacred number of completion and balance).

· That this harmonic series encapsulates the frequencies of 432, 540, 360 and 144 which all feature in geometry as the sum of angles in platonic solids, or the size of the sun in relation to the moon, etc.

· Before the discovery of this harmonic series based on B-flat = 7.2 Hz, it was not thought that there was a harmonic series that encapsulated all these frequencies

· That, in retrospect, most of my favorite music has always been in the “magic keys”

· That  the “cosmic year” of 25,920 years for the Earth’s full cycle through the precession of the equinox relates directly to our frequency for C at 259.2 Hz (determined as the 9th of our B-flat – or a fifth (times 3) of a fifth (times 3 again) of our B-flat of 7.2 Hz) – and that this number also relates to the the Fibonacci number of 1.61 squared, which equals 2.592

Together, this is a combination of luck, witnessed physical phenomena, historical alignment, inspiration by others on this same quest and aesthetic enjoyment – the perfect combination – if you’re a collaborative, scientific aesthete like myself!  It shows that we should re-examine what music is, what frequencies should – and should not – be played; hopefully to restore our planet to the harmony that our vibrational consciousness and our vibrational energy should be attuned to, for a peaceful, just, loving and caring society – which honors the natural world, and seeks to do all in its power to conserve, nurture and love our planet, our co-inhabitants, and ourselves.

I hope we’ll get some feedback and contributions from others (or any kind of acknowledgement really) – in the ongoing human movement back to harmony.

I accept that my ability to draw traffic to this blog is limited.  So, please do us all a favor and share this with your friends – and your enemies, why not?!

APPENDIX

PYRAMID RESONANCE

A technical walk-through of the resonance of the pyramids of Cheops in Egypt:

The author, Christoper Dunn mentions several resonant points:

· “resonant points around” 2.5 Hz (F is 2.7 Hz)

· “Around 90 Hz I observed a strong room mode” – F is at 86.4 Hz.  F-sharp is 90 Hz

· “…and sweeping at 1.1Hz/sec — some real energy was transferred.” 1 Hz is approximately a C. 1.1 Hz is approximately a C-sharp.

· “What really made everyone get up and run to the exit was the resonance near 30 Hz” – B-flat resonates at 28.8 Hz. B is approximately 30 Hz.

· “It also appears that any wind pressure across the Pyramid’s internal air shafts, especially when the Pyramid was new and smooth, was like blowing across the neck of a coke bottle. This wind pressure created an infrasound harmonic vibration in the chamber at precisely 16 Hz.” – C is at 16.2 Hz.

The author also notes,

“Being a musician myself, I was especially interested to discover a patterned musical signature to those resonances that formed an F-sharp chord. Ancient Egyptian texts indicate that this F-sharp was the resonant harmonic center of Planet Earth. F-sharp is (coincidentally?) the tuning reference for the sacred flutes of many Native American shamans.” 

This is of interest, but the author’s conclusion that his findings indicate a resonance around F-sharp, when the frequencies he reports themselves indicate the key of F instead, is perhaps an example of the mind drawing the conclusions that fit a pre-conceived model, rather than reporting the facts and letting the model present itself.

Nonetheless, the author’s recorded measurements seem to align with our theories around B-flat and F.

It’s not clear to me whether the Pyramid was created as a beacon of historical knowledge, as Graham Hancock has written, or as a mechanism for generating harmonics for good (or bad) purpose.  But that these harmonics are present along with the other geometry of the place does indicate the knowledge of the principles of universal harmony, and the intent to align with them.

SONIC GEOMETRY

The video by Eric Rankin on “Sonic Geometry” is very compelling and correlates the same frequencies we have found for F-sharp (360 Hz) and C-sharp (270 Hz) and A (432 Hz) to natural phenomena including the platonic solids, the diameters of sun and moon and the “great year”.  The video presents:

· 2-dimensional shapes whose inner angles in degrees add up to multiples of 180 (F#, in Hz):

· Triangle (180)

· Square (360)

· Circle (360)

· Hexagon (720)

· 2-dimensional shapes whose inner angles in degrees add up to multiples of 540 (C#, in Hz):

· Pentagon (540)

· Octagon (1080)

· Flower of life (6 circles) = 2160

· 3-dimensional forms whose inner angles in degrees add up to multiples of 360 (F#, in Hz)

· Tetrahedron (720)

· Octahedron (1920)

· 3-dimensional forms whose inner angles in degrees add up to multiples of 540 (C#, in Hz)

· Cube (2160)

· Phenomena relating to multiples of (or numerological similarity to) 144 (D) and 432 (A):

· 12 x 12 = 144 Hz = D

· 2160 (C#) :

· 2,160 = diameter of the Moon (in miles)

· 2,160 x 12 = 25,290 = The “great year” (how many Earth years it takes for the precession of the equinoxes to complete one cycle, through all 12 signs of the zodiac)

· 25,920 / 60 = 432 (A)

· 432 (A) x 2 = 864 x 1,000 = 864,000

· 864,000 diameter of the Sun, in miles

· 864,000 number of seconds in a day

What is interesting about this video is that at 12 minutes, 50 seconds – the narrator states that “the tuning method required to reveal geometric shapes is based on a mathematical grid, rather than mathematical ratios.”  In other words – that author has not found a musical harmonic series which contains the numbers 540, 360, 144 and 432.  But the harmonic series that we summarized above in table 7 actually does support all of these frequencies – as it happens! And our harmonic series also retains the numerological alignment to the number 9 described in the video.

So, this is an example of where simply by labeling the frequency 432 Hz with the note “A”, people assume that the A-note should be the foundation of musical harmonics.  But it is not.  See this section which compares the harmonic series derived from A=432 Hz to the harmonic series derived from B-flat=460.8 Hz.  As we have discovered above, the correct harmonic starting point is B-flat = 460.8 Hz (and, if you’re just tuning in, 4 + 6 + 8 = 18 = 9).

If you use a frequency of 460.8 Hz, as a B-flat – an octave of 7.2 Hz which I discovered as creating a “still point” of zero beats in relation to the non-audible interference frequencies around it – you have a basis which is in alignment with all the amazing things identified in the video – plus it’s actually musical – you can actually play perfectly harmonized music based on that harmonic series.

I hope this exposition has been clear and useful.  Please explore some of the other sections of the site for other details – such as the Solfeggio, etc.  And remember to provide some feedback in the blog section.

Thanks,

Julian Shelbourne, January 1, 2018

https://harmonicsofnature.com/

The Sun is D!

There are certain frequencies we are quite certain about in this web-site: Basically, the two I found, and the frequency of a Day which they are based on. Is there any other cosmic evidence we could find? Well, yes: apparently, the Sun resonates at a D frequency in this same Harmonic musical scale.

To recap:

1. The frequencies I found which seem to beat against an un-acknowledged background electro-magnetic Earth resonance (see home page and video).

· They are B-flat frequency of 7.2 Hz (and 230.4 Hz)

· F frequencies of 5.4 and 10.8 Hz (and 345.6 Hz)

2. A C of 259.2 Hz, which is the 3rd-harmonic of the F.

· A frequency like F that is strong enough to exhibit the “nodal still-point” behaviour must also be strong enough to generate its own 3rd harmonic.

3. The E-flat frequency, directly a 3rd-harmonic below that B-flat frequency

· This corresponds to one beat every ancient Helek = 0.3 Hz, 9.6 Hz and 307.2 Hz.

· Indicating that the ancient Hebrews and Babylonians who developed the calendar and time system understood the importance of this frequency.

4. An A of 432 Hz

· Which is the 5th harmonic of that F (major-3rd interval, 345.6 Hz x 5/4 = 432 Hz)

5. A D of 288 Hz

· Which is the 5th harmonic of that B-flat (major-3rd interval, 230.4 Hz x 5/4 = 288 Hz)

6. And, here we’ve explored the fact that all these frequencies derive from a G of 388.36148148 Hz which is an octave of one beat every 86,400 seconds, also known as a Day!

7. Also, from that page, we know that in order to get from the E-flat to the frequency of a day, you have to go down in 3rd harmonics to

· A-flat (409.6 Hz)

· Down to C-sharp (273.07 Hz) – also corresponding to one beat per minute, and 1-degree of rotation of the Earth

· Down to F-sharp (364.09 Hz)

· Down to B (485.452 Hz)

· And down to E (323.63 Hz)

· And down a 5th-harmonic from B to G to give us the Day frequency of 388.36148148 Hz

So, so far so good.

Well, strangely enough, the Sun is a D: NASA has released a “sonification” of the Sun, in which they have recorded the electro-magnetic frequency of the Sun and converted this into sound. You can hear that here:

Now, this is quite a low hum, and there’s a bit of a warble to it, but I wanted to explore what frequency and note it is.

So, I created this track.

1.

At first, you hear the original NASA Sun Sonification sound

2. At 10-seconds I bring it up an octave

3. And then at 14 seconds, a 2nd octave.

4. Then at 30-seconds, I fade in the sound of a sine wave playing a D frequency of 576 Hz, which is the 5th harmonic of the “magic” B-flat frequency we discovered
There’s a slight warble, but it’s pretty close – so next we explore whether it’s the Sonification that’s warbling, or if we are slightly out-of-tune at 576 Hz.

5. At 36-seconds, I try a D-sharp – which sounds too high.

6. And then at 41-seconds, a D-flat (which sounds too low) – both showing that it’s the D which is the closest match.
So, then it’s a question of which D.

7. So, at 50-seconds I change the D from 576 Hz to 582.5444 Hz (which is an octave of the D corresponding to one vibration every 5 minutes). That seems to make it less in-tune than 576 Hz

8. So, at 1:01 I try a D which is derived from a G of 388.8 Hz (583.2 Hz)
All this indicates that the “warble” is the Sonification (or the Sun) itself and not our D note of 576 Hz being out of tune.

9. So then at 1:07 I go back to 576 Hz

10. At 1:36 I remove the Octaves from the Sonification itself

11. The rest of the track is playing different octaves of D as 576 Hz, like 288, 144 Hz and a few other frequencies from my Bb myxolidian scale.

12. Finally, you hear just the original Sun Sonification again

So, this tells us some interesting things:

· The Sun is resonating at harmonics of 9 Hz (9, 18, 36, 72, 144, 288, 576 Hz). 9 is a significant and cosmic number

· The D-note for the Sun is not one of the 3rd-harmonic frequencies for D. Instead, at 576 Hz, it’s the 5th-harmonic (that is, it has a major-3rd interval relationship to our magic B-flat frequency).

· This in turn indicates that underlying the reality we can see and measure (like the frequency of the Sun) there is a more fundamental set of numbers and frequencies (like our B-flat 7.2 Hz and F 5.4 and 10.8 Hz frequencies) from which physical reality seems to be harmonically generated. Either that, or reality manifests top-down, so that the major-3rd D frequency is what generates the B-flat frequency below it.

· In a harmonic scale, there is always a point where the 3rd-harmonic you’re hoping for has been taken by a note that is the 5th harmonic of something else.

· For example, D is the 3rd harmonic of G. So, when you’re playing a G, you hope that the 3rd harmonic is going to be a D that is the 3rd-harmonic of that G

· But if that D is already the 5th harmonic of your B-flat, it’s not going to also be the 3rd harmonic of your G. The mathematics just doesn’t align

· But, if the Day is a G of 388.36148148 Hz, and the Sun is vibrating at a D of 288 Hz, then although this G and D don’t exactly “line up” as 3rd harmonics – what we see is something fundamental to our Solar System: This G, and this D do coexist in the “harmony of the spheres”.

· If you don’t like hearing that G frequency and that D frequency together, move to another solar system!

Finally, some medical advice: remember to take your vitamin-D!!

Here’s a bit of fun using this tuning, overlaying the Sun Sonification raised by just an octave:

Oh, and Tune your music correctly! I’ve been exploring the use of Melodyne as a way of converting existing Master recordings into this harmonic tuning.

This B-flat major scale I’m using therefore is comprised of the following frequencies:
B-flat 230.4 Hz
B 485.452
C 256
C# 273.066
D 288
Eb 307.2
E 323.63
F 345.6
F# 364.09
G 384
Ab 409.6
A 432

Other Natural Noises

Recently, I’ve been trying various natural sounds and overlaying it with the harmonic, Earth-tuning scale. You might enjoy some of these:

https://on.soundcloud.com/3L19V

Using Earth Harmonic tuning

Solfeggio Harmonics

 I never understood the Solfeggio.  They don’t make any kind of playable musical scale – they don’t seem to be harmonics of each other, you can’t create a melody out of them and they seem to have no relation to any other measured resonance. 

But with some prompting from friends I read through Len Horowitz’ Book of 528.  The main thing I learned from this is that Dr. Joseph Puleo had found the Solfeggio numbers in the Biblical Old Testament Book of Numbers.  

Well, it seems that in ancient times, the Minute was divided into 18 Helek, and the Second was not used until much later, perhaps the 16th Century. So, if the Solfeggio refer to vibrations, they’re going to be vibrations per Helek, not vibrations per Second.  

The Solfeggio number 528, for example may be a sacred number – but to hear it, we need to convert it from vibrations per Helek to vibrations per Second.

There are 3.3333-recurring seconds per Helek, so 528 / 3.3333 seconds = an octave of 316.8 Hz.

Now, 31,680 Miles is the perimeter around the earth, as well as the circumference around the Earth going through the middle of the Moon if the Moon was resting on the Earth. The following illustration is from John Michell’s book, Sacred Geometry – How The World Is Made.

Interestingly:

· 5040 miles (the radius from the centre of the Earth to the centre of the Moon) = 1 x 2 x 3 x 4 x 5 x 6 x 7

· And 7920 miles, (the diameter of the Earth) = 8 x 9 x 10 x 11

These number are all multiples of 720:

· 31680 (perimeter of Earth) / 720 = 44

· 2160 (diameter of Moon) / 720 = 3

· 5040 (radius of Earth with Moon) / 720 = 7

· 7920 (diameter of Earth) / 720 = 11 (and musically, 11 is an octave of 22)

So, all the harmonic magic of the ratio of size of the Earth and Moon, and Pi, can be understood as simple ratios.

You will recall from school that 22/7 is an approximation of Pi – so Pi (3.141 etc etc),the ratio from which the circumference of circles can be calculated, is simply the ratio of the Earth diameter (7920 miles) to the Earth-Moon radius (5040 miles)

(7920 x 2) / 5040 = 3.142857 142857 recurring = geometric Pi

· Interesting things about the number 720:

· Our B-flat frequency is 7.2 vibrations per second

· 216 vibrations per second (which is an octave of A = 432 Hz), is the same thing as 720 vibrations per Helek

· (720 / 3.3333 seconds = 216)

· 2160 miles is the diameter of the Moon

· 2160 vibrations per Helek is 648 Hz, an octave of the Solfeggio E at 324 Hz

Going back to the Mi Solfeggio tone of 528 vibrations per Helek (528 / 3.3333 seconds = 316.8 Hz):

· 316.8 Hz is the 11th harmonic of the B-flat frequency described on our home-page at 7.2 Hz which we know has an electro-magnetic interaction with sound, and is a sub-harmonic of the daily, gravity-driven rotation of the Earth.

· 7.2 Hz x 11 = 79.2 Hz

· 79.2 Hz x 4 = 316.8 Hz

The combination of a base frequency and its 11 harmonic has been used to selectively destroy cancer cells in the living body.  

Let’s consider whether all the Solfeggio frequencies might actually be encoded as vibrations per Helek, and are 11th harmonics of some underlying frequencies:

So, as vibrations per Helek instead of vibrations per second, the Solfeggio 528 (“Mi”) translates precisely as the 11th harmonic of our B-flat – as 316.8 Hz

And also, the Solfeggio 396 (“Ut”) translates precisely as the 11th harmonic of the Earth F frequency of 345.6 Hz, (475.2 Hz).

What are the chances of this!!?? The two frequencies I had happened to find in 2016 on a tone-generator app on my iPhone as being “non-beating” nodes against the background hum of Creation, happen to have been encoded in the Biblical Book of Numbers as their 11th harmonic in vibrations per Helek.

If you feel some power in 528 vibrations per Second, try instead listening to 528 vibrations per Helek, which is (528 / 3.3333 Seconds) = 316.8 Hz.

To celebrate – here’s a proper “528” track, where “528” is not vibrations per Second, but vibrations per Helek. And is therefore actually 316.8 Hz. The track itself is by my good friend Craig Pruess, who has adopted these frequencies for his latest work. And I provided some slow 11th harmonic frequencies for your general health – hopefully!

While the 528 and 396 numbers are precisely the 11th harmonics of the two frequencies we described on the home-pager, it’s also interesting in the chart above that the Solfeggio number 741 (“Sol”) is very close to the 11th harmonic of our E frequency of 323.63 Hz (323.3).

And also, “Re” translates from 417 vibrations per Helek to 363.9 vibrations per second (close to our F-sharp frequency, 364.088 Hz).

Now, the other numbers: Fa (639) and La (852) don’t yield anything from our harmonic scale that I can tell as 11th harmonics. But as basic frequencies they are close to one of our G frequencies (383.4 vs 384 Hz), and one of our C frequencies (256 vs 255.6). This here’s a track which, as I recall, uses all these frequencies – and there is a certain sweetness to this tuning:

The frequencies I’m using are a Bb myxolidian scale like this:

B-flat 230.4 Hz
B 485.452
C 256
C# 273.066
D 288
Eb 307.2
E 323.63
F 345.6
F# 364.09
G 384
Ab 409.6
A 432

In summary, as far as the Solfeggio goes:

· Everyone is listening to them wrong !

· When converted from vibrations per ancient Helek to vibrations per Second they reflect harmonics of the daily rotation of the Earth

· Somehow these frequencies are encoded in the Bible – if that is where Dr. Joseph Puleo and Len Horowitz found the Solfeggio numbers. And even if they just made the Solfeggio numbers up – it’s an amazing coincidence that converted from vibrations per Helek (3.3333-recurring seconds per Helek) to vibrations per Second, they are precisely 11th harmonics of the “still point” Earth frequencies I had discovered in a Johannesburg hotel room!

Below, we’ve also explored Beats Per Minute derived from these frequencies – for musicians looking to build tracks which connect their beats and rhythms to the resonance of our Planet. When the musical bass-line is resonating at a harmonic of your beat, then the music and the beat become one – and that’s incredibly powerful.

https://harmonicsofnature.com/solfeggio/

WHATS NEW AND EXCITING AT S.O.S ?

"As I was dialing through these low frequencies,

I noticed something strange – as I turned the dial

to make the tone lower, there was another

whooshing-thumping sound that was speeding up

– until I reached a point at 10.8 Hz where the whooshing

stopped – and just sort of hovered there." 

“Even though A=432 Hz is part of the harmonic series of B-flat and F – it’s not possible to go the 

other way and generate the correct harmonic frequencies for B-flat and F from an A.”

https://harmonicsofnature.com/

SOS users / members and I have noticed this type of phenomena in some of

our SOS frequency tracks over the last number of years. Until now, having

read this, I hadnt seen this sort of effect anywhere else.... very cool to be
reading about this sort of thing through another persons lense and experience....

"VICE" MAGAZINE DESCRIBES US ; "As for the frequencies themselves, Donald Adams,

a mathematician and former Microsoft software engineer from Edmonton, created them under

his company Sound of Stars. Using a huge database of research from the alternative and

contemporary health scene, he created mathematical maps of the different states of the brain

and applied them to an algorithm, which spat out the frequencies. His catalogue mostly deals

with healing and eliminating negativity. That's how the idea came of using it at parties.

I gave it to a friend, DJ Noor, just to experiment with his own creativity, but then it led to the

idea of us experimenting with audiences." 

https://www.vice.com/en/article/qkazgw/canadian-electromagnetic-instrument

9. CANCER AND TRI-TONES
So, here’s a fascinating thing. A group of researchers just discovered that by playing

two hyper-frequencies (between 100,000 and 300,000 Hz), they can destroy up to 60%

of cancer cells, so long as “the high frequency [is] exactly eleven times higher than the low”.

A frequency eleven times higher is, guess what? The tri-tone.

To put this into the context, if my low note was 7.2 Hz (a B-flat), 11 x 7.2 Hz = 79.2 Hz.

An E happens to be 81 Hz. That’s pretty close. And an E is the tri-tone of a B-flat.

In other words, these scientists have discovered that, in the hyper audio range of

100,000 to 300,000 Hz, you can kill cancer cells by blasting them with tri-tones.

So, what exactly was the church protecting us from in the Medieval period?

The “devil” or something that can be used for health and well-being?

A lot of jazz, and the work of Richard Merrick is centered on the notion of the tri-tone.

Perhaps there is a power in them there tri-tones!

https://harmonicsofnature.com/solfeggio/

==============================================================

( try tritones )

.........................................................

ASK ME MORE ABOUT TRITONES ; doc_starz@yahoo.com

==============================================================

WHY 432 HZ AS A REFERENCE PITCH IS WRONG

“…the idea that the foundational frequency of our harmonic series should be an A.”

B-flat as the reference pitch

“magic frequency” of B-flat = 460.8 Hz

….ancient instruments, and even today’s modern brass instruments, use F and B-flat as

their reference pitch. …..only B matches the frequencies generated from the harmonic

series of B-flat.  Even F – which should be an octave of our other magic frequencies 

of 5.4 and 10.8 Hz has been dis-figured from 345.6 (where it should be, and to which

the ancient Chinese bells and cymatics were centered) to 337.5 Hz.

…..evidence that A should not be the reference pitch – just as we saw that the ancient

Egyptian flutes didn’t even include the note A in their range.

https://harmonicsofnature.com/b-flat-versus-a-as-the-reference-pitch/

DOES OBJECTIVE MUSIC EXIST? Gurdjieff et al;

(This was a fascinating post made to the older SOS group a number of years ago - sharing here.)

"I recently read in Gurdjieff's "Meetings with Remarkable Men" in chapter VII, called "Prince Yuri Lubovedsky" page 128 about music. Gurdjieff states that objective music exists, e.g. in certain monasteries by monks chanting. Gurdjieff himself, so I have read, was able to affect a whole audience in whatever mood G. wanted to, by playing his accordion.

The numerous reports about the soothing or comforting effect of music played for plants, animals or unborn babies and patients in general anesthesia, may indicate that objective music does exist. Read more about music and plants..... under planetary conjunctions, there can be seen a connection between the Just Intonation scale and phenomenon in Nature and in our Solar System. In the human's hearing especially the octave recognition and the dissonance and consonance concept due to the critical band and the beats of harmonics, basically sets the distribution of tones in a scale.

http://vaczy.dk/htm/objectiv.htm

http://objectiveart01.tripod.com/

https://www.youtube.com/watch?v=8U-wcjqcCBI

Gurdjieff on Planetary Influences*** a video by Heracles V.

https://www.youtube.com/watch?v=oPooX6B4vow

and

How 2 Harness the Planetary Frequencies 4 Personal Transformation

https://www.youtube.com/watch?v=Ro01jhR_wJk&t=535s

SEE LINKS ;

http://whatmusicreallyis.com/papers/sacred_sounds_scale.html

https://web.archive.org/web/20160524185910/http://www.electrod.me/the-International-organization-for-numerical-musical-tuning

https://web.archive.org/web/20200202133222/http://whatmusicreallyis.com/research/tuning/

http://whatmusicreallyis.com/papers/

http://whatmusicreallyis.com/papers/hearing_nature.html

The Sacred Sounds Scale: Harmonizing 432, 528, 424 and 440 Hz into a Single Tuning.

There is one tuning in which the frequencies 432, 528, 424 and 440 Hz can peacefully coexist. The scale...

https://web.archive.org/web/20181201113946im_/https://www.aesdnet.work/sites/default/files/field/image/wmri_3s_harmonic_tone_circle.png

https://web.archive.org/web/20181201113946/https://www.aesdnet.work/blog

UPDATE : Following are comments from the originator ;

My question to him ;

“I had a question, while reviewing a link of yours ;

https://web.archive.org/web/20201010124608/http://whatmusicreallyis.com/research/tuning/

I saw this diagram ( see attached graphic )

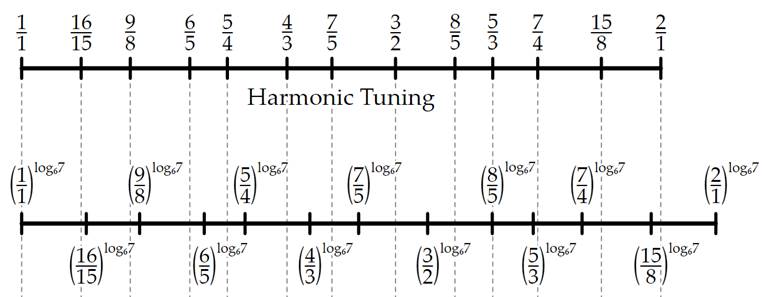
I had a couple of questions about some of the math expressions there, for example it shows ;

5/6 subscript 6, to the power of 7

In some of your other docs you show taking a ratio and taking its natural log and then multiplying it by 1000

In the example of 5/6 subscript 6, to the power of 7, are you taking the log using a 6 base?

My apologies but Im not following what ; "5/6 subscript 6, to the power of 7" would produce exactly?

Im probably missing something simple and obvious

Do you mean 5/6 to a log 6 base and then raised to a power of 7 ? “

His Answer ‘

“That section of the study is concerned with "Creating Consonant Artificial Tunings" and I give examples of stretched and compressed tunings, derived from their respective deviated series of harmonics.

These examples, as depicted in the graphics, stretch the perfect harmonics so that the deviated-stretched series #6 coincides with harmonic #7, respectively compress the perfect harmonics so that deviated-compressed series #7 coincides with harmonic #6. That's why all examples take log 6 and 7 from the log base 7 and 6.

So (6/5)^log₆7, also written (6/5)^log6(7) will stretch the harmonic tone 6/5 by raising it to the power "logarithm in base 6, of 7".

As a side note, there is no 5/6 sonic entity on that page — you probably mean 6/5.

Please don't bother with that section, it's a mathematical curiosity not worth exploring, unless you want to write something musical using artificial tunings. The links to actually hear these tunings work if you remove the header from the link (i.e. this "https://web.archive.org/web/20201010124608/").

Here they are, cleaned:

Play the Total Resonant tunings using these timbres on the Terpstra Keyboard WebApp:
n=log₆7 Stretched
n=log₇6 Compressed

In harmony,
Bo“

……………………..

The SOS perspective on 432 is described here ; 

https://soundofstars.org/432.htm

See the "PYTHAGOREAN COMMA" at the SOS link provided ;

Chinese prince Chu Tsai-yu in 1596 CE calculated even semitones to a correct accuracy of nine
decimal places, a feat that without calculus required extracting the 12th root of numbers containing
as many as 108 digits!

A Middle Path Between Just Intonation and the Equal Temperaments

RICHARD MERRICK ;
"y = 1.013317471 // The Pythagorean comma to 3 places
58 The associative property of the INTERFERENCE function
yields the y value of 1.013651449

https://soundofstars.org/pythagoreancomma.htm

NEW “EXOTIC TECH” ARTICLES

FULL ARCHIVE VIA GROUP ACCESS

RECENT ( CURRENT ) ;

DNA REGENERATION :  INCREASING THE LENGTH OF TELOMERES

ANTI-AGING EXOTIC CUTTING EDGE TECHNOLOGIES

HOW TO TUNE YOUR ROOM & FIND THE RESONANT FREQUENCIES OF A STRUCTURE

THOUGHT IS ELECTRIC, EMOTION IS MAGNETIC

QUANTUM BIOLOGY & THE SECRET OF BLUE LIGHT

GENETIC KEYS to Spirituality : CD38 & VMAT2

WHATS NEW AND EXCITING AT S.O.S ?

……………………………………………………………………………………………………….

CAUSES & TREATMENT METHODS FOR ALS LOU GEHRIGS DISEASE,

DEMENTIA, ALZHEIMERS, STROKE LIKE INCIDENT

These documents outline key considerations for the three main health issues of ;

ALS – LOU GEHRIGS DISEASE

DEMENTIA / ALZHEIMERS

STROKE LIKE INCIDENT

ALS METHODS 

https://soundofstars.org/alsmethods.htm

ALS CAUSES

https://soundofstars.org/alscause.htm

……………………………………………………………………………………………………….

Plato and Frequencies

Plato “imagines artistic inspiration as an electromagnetic field” and refers to unethical symmetric

mathematical information electromagnetic wave-fronts being capable of inducing disease, as a

“demonizing of art” (Morton T. 2012). The mathematical programming of gambling machines

using electromagnetic sound and colour vibrations to induce heroin-like addictions leading to

unethical states of financial and moral bankruptcy supportsMorton’s Science-Art research

REPLICATING MOLECULAR MAGNETIC FIELDS

https://soundofstars.org/replicatingfields.htm

FREQUENCIES OF THE GEOMETRY OF MIND

https://soundofstars.org/frequenciesofmind.htm

FREQUENCIES OF NEUROBIOLOGICAL RESONANCES & CEREBRAL BREATHING

https://soundofstars.org/enzymefrequencies.htm

USING SOUND TO CONTROL ENZYMATIC REACTIONS

https://soundofstars.org/enzymefrequencies.htm

ELECTROMAGNETIC PATTERNS OF CONSCIOUS ENERGY

https://soundofstars.org/consciousenergy.htm

ALUMINUM: HOW TO REMOVE WITH SILICA

https://soundofstars.org/aluminumremoval.htm

NEW - FREQUENCIES OF ATOMS

- TRANSFORMING THE SPECTRAL LINES OF EACH ELEMENT INTO A MUSICAL TONE

https://soundofstars.org/atomsongs.htm

WHATS NEW AND EXCITING AT S.O.S ?

……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

WHATS NEW AND EXCITING AT S.O.S ?

……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

The Fourier Transform in Your Eyes

“… the lens took rays that were global and made them local. “

the phase is where you are in the cycle of the wave: are you in a peak, a trough, the middle,

etc. But for this derivation, just know that it’s the stuff to goes into the exponent of the complex

exponential.

The transform is fundamental tool in science, but also is how your eyes see the world.

Equation 2: the wavevector definition, where the unit vector n points in the

direction of propagation. λ is the wavelength of light. where n is a unit vector pointing along the ray.

Because of the k-label, it’s also standard to call these k-vectors. This is the k goes into our wave

function exp(ikr).

https://www.cantorsparadise.com/the-fourier-transform-in-your-eyes-84cfe0fa31b4

PETER KINGSLEY: Parmenides and Empedocles lived just before the time in Western history when, with Plato and the influence of Aristotle’s disciples, we start to get the general notion that the senses lie. And because of this idea they were completely misunderstood.

P: So this is not a new idea.
PK: No, no. It’s implicit even before Plato, and later Greek philosophers formulate it very clearly: the senses are liars. Now Empedocles also begins his teaching poem by saying that the senses lead people astray. And so does Parmenides before him. But people don’t really read what they say. Instead they think: well, Parmenides and Empedocles tell us the senses are unreliable therefore we have to find truth through some other means.

It sounds very logical. The trouble is Empedocles and Parmenides never said that. What they said is that the senses aswe know them are unreliable, because we were never taught how to use them. Empedocles in particular was very specific. He explained that our senses are still closed. For him, we humans are plants: human plants. Actually we are seeds and have not yet become plants. We have not budded yet, have not yet started to open and blossom. We have the potential to become full human beings but the potential has not been realized. And I find this amazing and terrifying, that someone 2,500 years ago—someone who was laying the foundations for all our philosophical and scientific disciplines—said we’re not yet human, because what he said then applies just as much to us today.

https://parabola.org/2016/11/01/common-sense-an-interview-with-peter-kingsley/

……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

WHATS NEW AND EXCITING AT S.O.S ?

ACCESS YOUR FREE FREQUENCIES AT THIS LINK ; 

http://soundofstars.org/welcome/

LEARN MORE ABOUT US ;

DISCOVER AND LEARN HOW & WHY THIS WORKS

RESOURCES & QUICK REFERENCE LINK

JOINING OUR ONLINE GROUP

TESTIMONIALS ; PHENOMENON : STORIES FROM YOU

HOW TO SHARE YOUR STORY WITH US

GUEST APPEARANCE ON RADIO SHOW

SCIENCE OF PEAK PERFORMANCE & VIBRATIONAL WELLNESS ;

QUANTUM CONVERSATIONS SHOW WITH LAUREN GALEY  - PART 1

https://www.youtube.com/watch?v=QvIgtvzi6Nk

QUANTUM CONVERSATIONS SHOW WITH LAUREN GALEY  - PART 2

Cymatherapy LAUREN GALEY SHOW PART 2 - QUANTUM CONVERSATIONS cymatics cymatic therapy frequencies

COPYRIGHT PROTECTION NOTICE, ALL RIGHTS RESERVED WORLD WIDE BY

DONALD ADAMS, 2007 to 2018. READ BEFORE ACCESSING AND USING

These files are for your personal use and protection and for your family.

ALL CONTENT IS COPY RIGHT PROTECTED AND MAY NOT BE DUPLICATED,

REDISTRIBUTED, EXHIBITED, INCORPORATED IN ANY WAY WITHOUT PRIOR

EXPRESS PERMISSION FROM DONALD ADAMS, THE DEVELOPER.  AN EXAMPLE

OF THIS WOULD BE, IF YOU ARE A DJ YOU MAY NOT INCORPORATE OUR 

CONTENT IN THE PRODUCTION OF ENTERTAINMENT CONTENT FOR YOUR AUDIENCE.

HEALTH AND WELLNESS PRACTITIONERS MAY NOT USE ANY 'SOUND OF STARS' 

FREQUENCIES ( INCLUDING THE CONTENT IN THIS VIDEO) IN THEIR PRACTICE FOR 

CLIENTS WHERE A COMMERCIAL TRANSACTION IS OCCURRING IN ASSOCIATION 

WITH OUR CONTENT WITHOUT FIRST PAYING FOR A USAGE LICENSE OR WITHOUT 

PRIOR PERMISSION FROM THE DEVELOPER. AN EXAMPLE OF THIS IS, IF YOU ARE 

PROVIDING MASSAGE THERAPY FOR A FEE TO A CLIENT AND YOU ARE USING 

OUR CONTENT IN THE BACK GROUND WHILE YOU PROVIDE THE SERVICE 

- THIS SORT OF SCENARIO IS A BREACH OF OUR USAGE TERMS AND IS PROHIBITED - 

YOU MUST FIRST SEEK EXPLICIT PERMISSIONS AND LICENSING PRIOR.

All files are copyright protected and may not be shared or redistributed to others and are strictly for your own personal use

Disclaimer: None of the information provided on this site or on this page-including information provided in any videos or reviews expressed by individuals or other third parties- is intended to communicate any medical information, and no products or devices described are natural health products or medical devices. For a full summary of the intended use of any products sold on this site, as well as more clarity on why none of our products are to be used for health related or medical purposes, (especially not as medical devices or health products), please carefully read through all of our disclaimers listed. To read all of our full disclaimers click here.

Video Disclaimer: Thank you for watching our video. Please note that all the information and views provided in this video is not to be construed as advice, and such information constitutes only the opinion of the presenter or individual expressing or communicating the information. We (Sound of Stars Frequencies - Donald Adams ) do not endorse, vouch for or encourage any of the opinions or views of those presenting information in this video, and such views belong only to those making them. Furthermore, we do not endorse or assert the reliability, accuracy, fitness for any purpose or truth of any information, products, services or statements shown in our video, and we expect that you, the viewer, will make a researched, personally informed and independent evaluation as to the truthfulness of any information presented in this video. Do also note that any device described in this video is not a medical device under any circumstances unless explicitly stated. Therefore, any such devices shown in our video are not displayed to cure, treat or remedy any health condition or illness. For any matters related to your health, do ensure that you consult your doctor for proper diagnoses and treatment. Any consumable products displayed in this video are also not regulated or approved by any regulatory agency, and therefore you should fully research the nature and contents of such products, as well as their regulated status in the region you reside, before taking any decision to obtain, use or purchase such products.