WHATS NEW AND EXCITING AT S.O.S ?
Chinese prince Chu Tsai-yu in 1596 CE calculated even semitones to a
correct accuracy of nine
decimal places, a feat that without
calculus required extracting the 12th root of numbers containing
as many as 108 digits!
- Joel Ellis Rea
http://mathforum.org/library/drmath/view/52470.html
A Middle
Path Between Just Intonation and the Equal Temperaments
https://sethares.engr.wisc.edu/paperspdf/Erlich-MiddlePath.pdf
https://sethares.engr.wisc.edu/papers/erlich.html
RICHARD MERRICK ;
............
"y = 1.013317471 // The
Pythagorean comma to 3 places
58 The associative property of
the INTERFERENCE function
yields the y value of
1.013651449"
............

SHARED PRIVATE
MESSAGE FROM AN ASSOCIATE ;
From: W,
Stephen <x@bsu.edu>
To: xxxxx
Cc: Nl, Jody <x@bsu.edu>
Sent: Tuesday,
January 10, 2017, 8:43:51 PM PST
Subject: Pythagorean comma
questions
W, Stephen has shared a OneDrive for Business file
with you. To view it, click the link below.
Hello XXXXX!
Im thrilled that Dr. Nagel
sent me your email, because its so rare that anyone wants to talk about the
Pythagorean comma at Ball State!
I will be able to answer all of questions, I'm sure, and point you to some
sources, although I may need to ask you what your deeper purpose is for using
the Pythagorean comma in the way that you propose. I also dont know how much
you know already, so if I explain something in too much detail that you already
know, I do apologize.
Let's go through the questions one at a time:
Something I'm not clear on however still, is 'where' and 'when' and how often
the comma is introduced?
Traditionally in just intonation, commas are used to indicate small differences
between two pitches that are already very close. Thus, the usual purpose of a
comma, is to cause those said two pitches to be perceived as one, in
whatever the desired tuning. (The name comma literally refers to splitting hairs.) For example, in 12-tone equal temperament, the
Pythagorean comma vanishes, and we can illustrate this with its fifths:
Twelve 12-equal fifths equal seven 12-equal octaves, while, in Just Intonation,
12 perfect fifths do not equal seven octaves exactly. Thus, the Pythagorean
comma is tempered out in 12-equal, and, in any tuning where 12 of a tuning's
perfect fifths equal 7 of that same tuning's octaves. It is also more
common in microtonality nowadays to write things in cents (there are 1200 cents
in an octave anywhere in the frequency range), because it:
(a) Allows one to add instead of
multiply, which is usually easier unless the fractional frequency ratios must
be preserved
(b) Allows one to compare intervals
to 12-tone equal temperament (100 cents is the 12-equal semitone)
(c) Allows one to see interval
sizes at a glance (takes care of the logarithm)
Tuning theorists have also
perfected the finer geometrical and algebraic points of temperament (extremely
expediently within the last two decades). Geometrically, illustrating a
lattice causes one to be able to see the relationships between the intervals in
question. A Pythagorean lattice, for example, is two-dimensional, with one
dimension representing a multiplication by 3, and another representing
multiplication by 2. A picture of a Pythagorean lattice is on pages 162 and 163
(or four and five) of the paper attached to this email. Thus, Pythagorean can
also be called 3-limit, as the highest prime number used in its frequency
ratios is 3. (5-limit harmony would correspond to using 2, 3, and 5 in
Just triads: the Just Major chord spelled in frequency ratios is spelled
like this:
(1/1 = Do 5/4 = Mi
3/2 = So)
Another thing to mention:
today's tuning theorists, if they do not represent an interval with cents,
will often represent it with the frequency ratio as a mixed number or a monzo (named after Joe Monzo),
depending on what is convenient. A frequency ratio is convenient with less
complex ratios, as it allows a glimpse into how Just-sounding the interval in
question is. Representing the Pythagorean comma as a fraction, and as a monzo, is also useful.
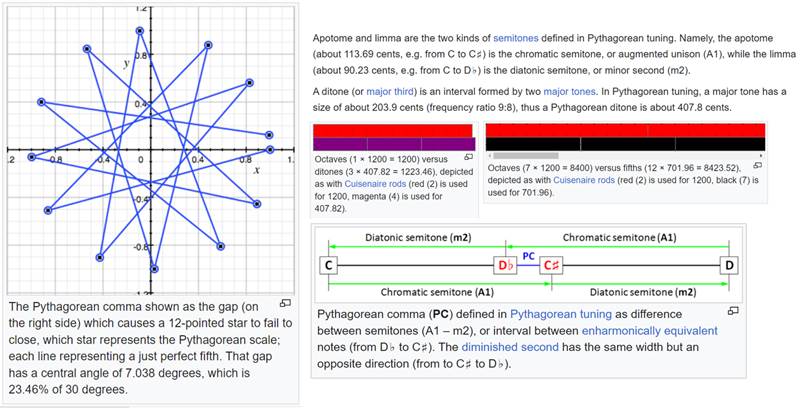
The Pythagorean comma is 531441 / 524288.
This comes out to about 23.460
cents.
Monzo: [-19 12]
(The conversion from frequency ratios to cents is the logarithm below)
CENTS = 1200 * log2 (f2 / f1)
And thus,
2^(CENTS / 1200) = f2 / f1
Each cent is equal to one step of 1200-tone equal temperament.
All rational numbers (Just) can be represented as a fraction, and will produce
a repeating frequency ratio, as well as irrational cent numbers.
All irrational numbers (Equal Tempered) cannot be represented as a fraction
(unless it is the octave or unison), and will produce an irrational frequency
ratio that extends forever, as well as rational cent numbers.
Thats why the values for a 12-tone equal tempered fifth are:
Frequency ratio (irrational): 2^(7/12) = 1.49830707688
Cent value (rational): 700 exactly.
And the values for a perfect fifth (used in Pythagorean tuning):
Frequency ratio (rational): 3 / 2 = 1.5 exactly.
Cent value (irrational): 701.955001
Monzo: [-1 1]
The Monzo just tells you the prime factorization of
the interval in question; positives are written in the denominator and
negatives are written in the numerator. All 3-limit / Pythagorean monzos are pretty simple since they only involve 2
(octaves) and 3 (tritaves, or, an octave + a fifth). [-19 12], the monzo for the Pythagorean comma, could be written out like
so:
(3)(3)(3)(3)(3)(3)(3)(3)(3)(3)(3)(3)
___________________________________________________________________
= 531441 / 524288
(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)(2)
This fraction also shows you the
difference between 12 perfect fifths and 7 octaves: The 12 perfect fifths are
multiplied, and, since a perfect fifth is 3 / 2, this causes twelve 3s to be
on top, and twelve 2s on bottom. Then, moving DOWN an additional 7 octaves,
allowing us to arrive at the almost-same note the
comma is at, puts the other seven 2s in the bottom, 12 + 7 = 19.
Most intervals I know (including commas) are represented this way. The Monzo is helpful when there is a lot of information that
cant be written as easily as a simple fraction (which is often). The monzo also tells you which directions to travel on the
lattice if you wanted to traverse that commas distance using its visual aid.
So to summarize where and when the comma is introduced, it is traditionally
used to eliminate a small difference between two notes in practical tuning
situations, known as temperament. (The Pythagorean comma, specifically, is one
of the best purely mathematical reasons to use 12-tone equal temperament,
and it's a big part of why a Chinese musician discovered 12-equal
first). I would also say that the Pythagorean comma is common
knowledge among microtonalists, because its such an important and well-documented comma.
I need to know 'when' to apply the comma value as multiplier to an input
tone.
Im curious as to exactly what you mean by this statement. Do you mean that you
want to resolve a Pythagorean-comma difference in just intonation when necessary by raising (or lowering) certain notes a comma? If
youre interested in that, I have a list of people to whom you could talk who
have better software chops / are themselves inventors of the software. Or do
you want harmonic progressions to drift by a Pythagorean comma? Or are you
looking to use the Pythagorean comma as a melodic interval of around 23 cents?
It seems like knowing when would be up to you, unless
there is a more specific question about the system.
While I found the below
information helpful initially, someone else mentioned to me ;
"... pitch space follows a log scale and isn't linear so we couldn't use
the comma to measure difference every 7th octave."
Im not sure what your friend
meant, but the fact that ratios and cents (or equal divisions)of
pitch are logarithmically related does not mean we cant measure things. Ratios
are always multiplied, and cents are always added. We can,
in fact, measure the difference every 7th octave, and
just did. We just have to be careful with units.
So HOW does the comma work and when do we apply it? And how
would this work in
regards to pitch space and log scale?
I think I told you the basics of
that above, but please clarify if I missed anything. Im confident I can direct
you to all of the information necessary if any is
missing.
If I want to take a frequency and
increase it by 'n' steps, where 'n' may
be as many as hundreds or
thousands, how do I construct a formula
that incorporates the log and the
comma correctly?
Dr. Nagel has told you how,
now perhaps I can also specify and include more information. He has
labeled (H/L) as a high and low note, the comma as C, and frequencies as X
and Y. Due to convention, I prefer to think of ratios as fractions (since it is
conducive to working with Just Intonation when small ratios are used), and I
prefer to leave frequencies out unless they are needed for some kind of special
application (which it looks like you are going to use.). I also use cents, and prefer to think of the comma as a ratio (in our
case, 531441 / 524288). Basically, if you are going up by a certain interval,
you multiply its ratio, and thats about it. So Dr. Nagels formula could be
even more generalized to read:
Y = X * (H/L)
also, if the comma is added into the mix, you would just have another ratio,
which you could write as two ratios:
Y = X * (H/L) * (H1/L1)
(H1/L1) for example, could be the comma, or (H/L),
whichever.
Another good reason to keep the frequency ratios as fractions is for cancelling
purposes (makes it easier to do the math of multiplying them without a
calculator, mostly, and lets you visualize the relationships and common factors
similarly in the way in which a monzo does).
I want to test value increase to hundreds and even many thousands of steps and
then view the result, using your modified Pythagorean values.
Do I just insert it once, so if the
hertz value Im working with is 333 Hz, do I just ;
333 Hz * 1.013651449 = 337.545932517,
then use that value as the input for my tables below?
Im not quite sure what youre asking. Perhaps we can discuss specifications
more once Im more filled in on your goals.
Based on what you might be asking:
(1) If you are asking about how to see a frequency a Pythagorean comma higher
than the original note, then yes
thats exactly what you do to find it.
Maybe you want to try it for a lot of different frequencies? For what use?
(2) If you asking about stacking more fifths to find other places where stacks
of perfect fifths are close to octaves: thats been done, and you can see the
values online as 3-limit commas. (For example, the difference between 53
perfect fifths and 31 octaves is called Mercators comma, and its tiny.)
Interested to hear your thoughts!
Some great microtonal resources online are Joe Monzos
website, Stichting Huygens-Fokker online, and the
Wilson Archives. The xenharmonic wiki is also a good
place to go if you want to track down a fractional ratio and know whats it is
called in the microtonal world - just type a fraction into the search bar with
an underscore instead of a slash mark; for example, you could type in the
Pythagorean comma by searching 531441_524288. (There are
many lists of commas on the xenharmonic wiki)
http://www.tonalsoft.com/enc/e/equal-temperament.aspx
http://www.huygens-fokker.org/index_en.html
http://www.anaphoria.com/wilson.html
http://xenharmonic.wikispaces.com/Comma
Hope this project goes well for you,
please ask me as many questions as you like,
Stephen Weigel
---------------
For the equal temperament scale,
the frequency of each note in the chromatic scale is related to the frequency
of the notes next to it by a factor of the twelfth root of 2 (1.0594630944....)
a = (2)1/12 = the twelth root of 2 = the number which when multiplied by
itself 12 times equals 2 = 1.059463094359...
The wavelength of the sound for
the notes is found from
Wn = c/fn
where W is the wavelength and c is the speed of sound. The speed of sound depends on temperature, but is approximately 345 m/s at "room
temperature."
Examples using A4 = 440 Hz:
C5 = the C an octave above middle
C. This is 3 half steps above A4 and so the frequency is
f3 = 440 * (1.059463..)3
= 523.3 Hz
If your calculator does not have
the ability to raise to powers, then use the fact that
(1.059463..)3
= (1.059463..)*(1.059463..)*(1.059463..)
That is, you multiply it by
itself 3 times.
Middle C is 9 half steps below A4 and the frequency is:
f -9 = 440 * (1.059463..)-9
= 261.6 Hz
If you don't have powers on your
calculator, remember that the negative sign on the power means you divide
instead of multiply. For this example, you divide by (1.059463..)
9 times.
https://pages.mtu.edu/~suits/NoteFreqCalcs.html
http://robertinventor.com/software/tunesmithy/help/cents_and_ratios.htm
https://www.notreble.com/buzz/2010/02/04/math-and-music-intervals/
http://mathforum.org/library/drmath/view/52470.html
https://pages.mtu.edu/~suits/notefreqs.html
Scales: Just vs Equal
Temperament (and related topics)
The "Just Scale"
(sometimes referred to as "harmonic tuning" or "Helmholtz's
scale") occurs naturally as a result of the
overtone series for simple systems such as vibrating strings or air columns.
All the notes in the scale are related by rational numbers. Unfortunately, with
Just tuning, the tuning depends on the scale you are using - the tuning for C
Major is not the same as for D Major, for example. Just tuning is often used by
ensembles (such as for choral or orchestra works) as the players match pitch
with each other "by ear."
https://pages.mtu.edu/~suits/scales.html
A table showing a comparison of
one meantone temperament with equal temperament can be found here.
https://pages.mtu.edu/~suits/etvsmean.html
Scales: Just vs Equal
Temperament (and related topics)
For the Just scale, the notes are
related to the fundamental by rational numbers and the semitones are not
equally spaced. The most pleasing sounds to the ear are usually combinations of
notes related by ratios of small integers, such as the fifth (3/2) or third
(5/4). The Just scale is constructed based on the octave and an attempt to have
as many of these "nice" intervals as possible. In contrast, one can
create scales in other ways, such as a scale based on the fifth only.
https://pages.mtu.edu/~suits/scales.html
https://pages.mtu.edu/~suits/justints.html
Musical scale based on fifths
Note that the "octave" for
this scale, the eighth note of the scale, should be a fifth above one of these
notes, and not the usual octave. The closest would be a frequency ratio of
2.027286, slightly larger than our normal octave. Various schemes have been
introduced to try to "fix" the octave for such a scale.
One can create a musical scale
based solely on the "fifth" and the octave. First, pick a starting
pitch, now go up a fifth (multiply the frequency by 3/2), then go up another
fifth and convert this back down an octave, go up a fifth from that - if the
result is beyond the octave, go back down an octave.
Mathematically, starting with a
pitch f0, the next pitch is f1 = 3f0/2, and f2 = (3/2)f1/2.
More generally, given the pitch fi, then
fi+1 = (3/2) fi if that result is
less than 2 f0
fi+1 = (3/4) fi if the previous
result was not less.
Of course, this process can be
repeated indefinately and
one will stop after a while to keep the number of notes in the scale
reasonable.
Here is a table which results
from that procedure. I have included more notes than we usually use for the
sake of illustration. Here f0 = 261.63 Hz was used as an example and
corresponds to "middle C." Frequency differences (in Hz) are based on
this f0.
https://pages.mtu.edu/~suits/fifths.html
Pythagorean Scale
https://pages.mtu.edu/~suits/pythagorean.html
Overtone Series
Since notes can be translated by
an octave by multiplying or dividing the frequency by 2, these overtones of one
fundamental define the notes C, E, and G. If we now make another string with a
fundamental frequency corresponding to E3 (655/4 = 163.75 Hz) and look at its
overtones, we define the notes B, and Ab. Starting with G3 (196.5 Hz), one gets
an overtone defining D. Starting with D, the notes A and F# are overtones.
Continuing the process, the notes of the scale are produced.
https://pages.mtu.edu/~suits/overtone.html
The 7th Harmonic - and how to
avoid it
The 7th harmonic will be at a
frequency 1.75 times that of the 4th harmonic. It would be a musical minor 7th
if it were 1.8 times the 4th harmonic. Hence the seventh harmonic is a very
flat minor 7th.
The total sound you get from the
string is a sum of the sounds from all of the
overtones present. If the seventh overtone is present, and it is played along
with other notes from the scale (particularly the 7th or diminished 7th of the
scale), a dissonance from this out of tune note is heard.
https://pages.mtu.edu/~suits/badnote.html
Pentatonic Scales
https://pages.mtu.edu/~suits/pentatonic.html
Dispersion
https://pages.mtu.edu/~suits/dispersion.html
(To convert lengths in cm to inches,
divide by 2.54)
Frequencies for equal-tempered
scale, A4 = 432 Hz
Speed of Sound = 345 m/s = 1130
ft/s = 770 miles/hr
("Middle C" is C4 )
https://pages.mtu.edu/~suits/notefreq432.html
Overtone series
One of the main landmarks in
ratio notation is the overtone series. One can start anywhere, but why one
starts from middle c, it goes
1,
2, 3, 4, 5, 6,
7, 8, 9, 10,
11, 12, 13
c, c', g', c'', e'', g'',
(a'' flat), c''', d''', e''', (f'''), g''', (a''' flat)
where the ones in brackets are in
the cracks between the keys of a keyboard.
These are the notes you get by
overblowing on a natural horn, or by touching the string in various places to
bring out the harmonics on a string instrument.
So, for example, we see from the
overtone series that the e'' is 5/1 .
To get it into the range of the
octave c to c', you need to go down two octaves, i..e.
divide by two twice, which drops it down to e = 5/4. So that gives us our major
third.
Then g' is 3/1 which drops down
to g = 3/2 which is our fifth. The 13/1 needs to drop down three octaves to
13/8 - that doesn't correspond exactly to any of the twelve equal notes, but is
a pleasant interval for those who have the taste for it.
So, to go up by a major third
from any frequency, such as from c to e, you multiply by 5/4. This is pretty
close to the 400 cents major third, a little flatter, and for those who get
used to it, the interval has a particularly sweet feeling to it in harmonic
timbres. A harmonic timbre is one such as voice, strings, etc,
which has a 1 2 3 4 5,... type overtone series.
To find the minor third, one looks
at the interval in the overtone series from the e'' to the g''. That is between
the 5th and the 6th overtones.
The ratio between these is 6/5 -
that is how one does it with ratios - instead of subtracting, you divide in
this case, you divide the 6 by the 5 to find the ratio from 5 to 6.
So, to go up a minor third from
any frequency, you multiply it by 6/5. E.g. why you go up a minor third from
440 hz, you get to 440*6/5 = 528 hz.
We can now see that when one is
working with hertz, then ratios notation is actually easier to use than twelve
equal temperament semitones or cents - it's harder to work out the hertz value
for an e flat exactly three semitones, or 300 cents above 440 hz than to find the herz value
for the pure minor third above 440 Hz.
http://robertinventor.com/software/tunesmithy/help/cents_and_ratios.htm
Math and Music: Intervals
adding intervals is equal to
multiplying frequency ratios.
This is a critically important
concept for the next steps where we apply logarithms. For those of you that do
not remember algebra, the logarithm of two multiplied values is equal to the
sum of the individual logs of each value e.g. log(ab)
= log(a) + log(b). Now we can do the following:
r3=r2*r1
log(r3)=log(r2)+log(r1)
i3=i2+i1
i3=log(r3)
i2=log(r2)
i1=log(r1)
Now we have a defined number for
the value of i. It is the log of the ratio of the
frequencies comprising the interval in question. The frequency ratio for any
given interval will be positive, but it may be greater than or less than 1. If
the value of r is greater than 1, then we know that 0 < f1 < f2 and the
interval is ascending (because f2 is greater than f1). Likewise
if 0 < r < 1 then 0 < f2 < f1 and we know the interval is
descending. Therefore the log of an ascending interval (with r > 1) will be
positive while the log of a descending interval (with r < 1) will be
negative.
So why is this useful? Well we know how to determine ratio of an interval formed
from other ratios. For example, if we knew one interval (r1) had a ratio of 5/4
(which if you know your overtone series, youll recognize as a major third) and
another (r2) the ratio 6/5 (a minor third) we can calculate the ratio of their
sum. So a major third (5/4) plus a minor third (6/5)
gives:
r1*r2=r3
5/4*6/5=3/2
The ratio 3/2 is a perfect fifth.
Do you realize what we just accomplished? We mathematically proved from a bare
concept that a major third plus a minor third gives a perfect fifth! I admit,
Im a big math/music geek, but thats awesome. A quick refresher for your small
integer overtone pitch ratios so you can try some other examples on your own (I
know youre dying to, dont pretend youre not):
Math and Musical Scales
Since an octave must have the raio 2:1 and there are 12
half-steps in an octave, each
half-step must therefore have a ratio of
2^(1/12),
2 raised to the 1/12th power, or the 12th root of 2.
Unlike even-temperament,
well-temperament
retains pure or nearly pure
fifths and thirds in several keys, while
sacrificing some of the purity in
other keys.
As a result, each key has
different "qualities" which are lost with
the homogenization effect of even
temperament. There was a reason
that, for instance, Bach's famous
"Toccata and Fugue in D Minor" was
in D Minor and not in, say, C
Minor or C# Minor or Eb Minor. None of
those would've had the effect he
was trying to produce. And, more to
the point, today's even-tempered
scale does not have the effect he
was trying to produce. Relatively
few people have ever heard any of
Bach's (or numerous other
composers', for that matter) music the way
they intended it to be heard.
Today, playing the Toccata and Fugue
in another key would sound the
same, only "transposed." But in
Bach's day, the quality of that
piece and its harmonies, and the
resulting emotional resonances,
would also change.
The well-tempered scales
demonstrated by Bach led to but are not the
same as today's even-temperament.
Actually,
the math behind all of this is fascinating. Why DO pitches
in perfect harmony in one key
become out-of-tune in another? The
answer lies in the fact that
going all the way around the Circle of
Fifths by starting with one pitch
and multiplying it by 3/2 (1.5)
twelve times with octave shifts
to keep the result in the same octave
does NOT produce the same pitch
as the note with which you started.
This discrepancy is called the
"ditonic comma." Its size is about 24
"cents" (a cent is
1/100 of an Even Tempered semitone, thus a
logarithmic scale that remains
the same regardless of the base pitch,
which Hz would not do). There is
also a "syntonic comma" based on the
fact that going up four fifths
around the Circle of Fifths does NOT
produce a true harmonic major
third (look at the "C#" line above: it
should have been 275, down an
octave from 550, which would be the
precise 5/4 multiple of A =
440Hz).
Resolving these
"commas" so that octaves remain octaves meant slight
compromises to the fifths (since
the ~24 "cents" of the ditonic comma
was for the whole Circle of
Fifths - Even Temperament, for instance,
subtracts about two cents [~24/12]
from each fifth to bring all the
octaves into tune) and more
substantial compromises to thirds. Some
tuning methods sacrificed fifths
for purer thirds, or kept some keys
in tune while creating bad-sounding "wolf intervals" in other keys
(for
instance, some resolved the ditonic comma by keeping
all but one
of the fifths pure and piling the
whole ~24-cent discrepancy on that
one "wolf fifth," while
others kept eight of the fifths pure while
putting a less-bad sounding
~6-cent [~24/4] on the remaining four
fifths spread either evenly
around the Circle, or placed so that keys
related to C sounded pure at the
expense of those further away -
another method kept six fifths
pure and put a ~4-cent offset on the
other six, again accounting for
the full ~24 [~6*4]). These latter
methods are the
"well-temperament" tunings that Bach and others were
familiar with - the ones that did
not result in "wolf" intervals.
Prior to Kirnberger
and others, the common tuning system for pipe
organs and other hard-to-retune
instruments was Mean Tone, which was
an attempt to average out the
comma using arithmetic mean. Again,
some keys would sound different
from others using this method, but
there would also be the
occasional "wolf". The most common of these
was the "1/4 comma mean tone."
This system is still used on some of
the European classic pipe organs.
There has been in recent years a
resurgence of interest in tunings
other than the Even Temperament
we've been stuck with for the past
couple of centuries, not only by
organizations such as SPEBSQSA (the
Society for the Preservation and
Encouragement of BarberShop Quartet
Singing in America), but also by
"purists" who want to hear the music
of Bach, Pachelbel, etc. the way
they intended it, and those who are
interested in various non-Western
ethnic scales. Go to any Web
search engine and type in
"just intonation" for a sample.
Justonic, Inc. is
a software company that has patented a method
for doing true dynamic just
intonation using modern microtunable MIDI
instruments. (I'm not associated
with them - I am a non-card-carrying
hanger-around of SPEBSQSA,
though.)
- Joel Ellis Rea
Editor's note: for "Pitch
and Temperment," see
http://debussy.music.ubc.ca/~courses/319/Notes/PitchAndTemperment.html
Today's even-tempered scale as we
know it
wasn't even perfected until THIS
century, simply because the human ear alone
and unaided can not possibly tune
to irrational pitch relationships. The
closest that can happen is like
piano tuners who first tune one note to a
reference pitch (say, A=440Hz), then
tune the lowest A to have a pure octave
relationship, then produce the
notes within one octave up of that A by
playing both them and the
next-lower key (starting with A#/Bb and the
previously tuned lowest A, which
[not entirely coincidentally] is the
lowest note period on an 88-key
piano) and counting the BEATS that result
from the ERRORONEOUS harmonic
relationship that is the Even Tempered scale
between those two notes. Once
that whole lowest octave is tuned, each
higher note is tuned by tuning it
to a pure octave relationship to its
counterpart in that lowest
octave. But even that won't be exact.
The CONCEPT of even-tempered
dates back quite a bit further (330 BCE to
be precise, by Aristoxenus of Tarentum, a student of Aristotle), but
couldn't be calculated properly
until calculus was invented, as it required
exponentials and logarithms
instead of simple ratios. Several amazingly
close attempts were made by the
Chinese, with Ho Tcheng-tien (370-447 CE)
creating a series of string
lengths for a scale of twelve approximately
equal semitones - the maximum
deviation from today's Even Temperament was
less than 0.1 semitone! Even
better was Chinese prince Chu Tsai-yu in 1596
CE (over a millennium later), who
calculated even semitones to a correct
accuracy of nine decimal places,
a feat that without calculus required
extracting the 12th root of
numbers containing as many as 108 digits!
Much of this info can be found in
the excellent book _The Story of
Harmony_, available from Justonic (it comes with their Pitch Palette
software, but can be purchased
separately).

REAL
PORTALS - HOW THEY AFFECT YOUR BODY
THE FULL STORY SHARED FOR THE FIRST TIME HERE
( ALL RELEVANT EXCERPTS & LINKS )
TOPICS
:
- PORTAL EXPERIENCES & SENSORY
EFFECTS
- SUPRANORMAL ANTI AGING &
REGENERATION EFFECTS
- THE MATHEMATICAL MODELS OF THE
PORTAL
- THE LIVING TECHNOLOGY
; "APHYSICAL DIMENSIONAL ACCESS MANAGER".
- THE DISSAPEARANCE OF THESE
SCIENTISTS AND KEY FIGURES
SEE ; https://soundofstars.org/portals.htm

Joe assigned me to the original
volunteer team testing the protoype.... great guy,
many amazing conversations
ahead of his time. Joe was really
onto something, I know, I witnessed it first hand along
with my team mates.
Despite the physical attack on
him and his lab, the constant critique, slander and oppression he faced I know
what he was doing actually worked..... another of the great ones I sorely miss...
Joe assigned me to the
'ANTI-AGING' team testing the A.D.A.M.
( Aphysical Access Dimensional Manager).
When ever we were exposed to the field emissions, it sure felt strange...
affected both the body and mind,
a really trippy sensation... and it worked! It
affected us all in a similiar and yet unique
fashion....
one guy who had a lot of grey in
his beard noticed in a very short period how the grey was fading
and the black was emerging again ....
Missing Dr Joe Champion.... Thanks Joe for including me on the A.D.A.M. Project... a
real honor to work,
serve and collaborate with you
and your team... thanks for all the support you gave my friend Doug!
Where
ever you are, hope all is well!
Joe and his laboratory were
attacked, he suffered significant brain damage, the last time I spoke with him
On the phone was after the
attack
he seemed to be coping but was still in recovery
. The last time I was
in contact
with him if I recall was between
2004 to 2007

ADAM is a living
technology ¬and the name is an acronym for "Aphysical
Dimensional Access Manager".
PJP: Please
explain what makes it a living technology.
JC:The central component of ADAM is a living protoplasma - a living entity. It lives inside of a
specific electromagnetic field that includes gold, platinum
and nickel probes. The plasma interacts with the computer on its own
determination. When it is contacted by the operator, it first begins the
process by trying to figure out, Why are you sending me signals? What do you
want me to do right now?
In essence, what were doing is taking a communication
in the form of a specific kind of mathematics from the physical realm and
popping it into the aphysical (non-physical) by using
the protoplasm. Then the protoplasm transmits the communication to a light-type
protoplasm and pops it from the aphysical back to the
physical. (skip down to the Supporting Science report
on this page for a more indepth explanation)
PJP: Now when you
say that the universal language is mathematical, is it numbers or is it more
like geometric symbols?
JC:Well, the problem is that no one is over there to know that. There is still
so much that we don't know. Its likely to be a series of complex algorithms
¬not simple computer numerology of zeros and ones. Its a multi-dimensional and
multi-tiered language. Even when you speak of light, light is in essence still
mathematical ¬ because light is a ray of colors.
PJP: Is there such
a thing as a language that goes beyond mathematics and is something we don't
even have words for?
JC:Even if it goes beyond mathematics it would have to be explained to us in
mathematics for us to be able to comprehend it.
PJP: How does this
apply to the ADAM technology and its ability to be so effective?
JC:Your long-term memory, my long-term memory and the long-term memories of a
few billion people on this planet are sitting in the same moving space ¬ in the
same compacted space in a non-physical (aphysical)
location. Everyones subconscious is sitting there collectively. The ADAM
technology has the ability to reach into that
non-physical location and locate specific memories.
Have you ever gone
down the road and you felt that you would see some body
you knew or you knew who was calling when the phone rang?
PJP: Sure. Lots of
times.
JC:The only reason you knew was because you got it from their mind that they
were thinking of you. This gave permission for your mind and their mind to join together. When the minds join at the subconscious
level, then you know whats going to happen.
PJP: Is that a way
of describing telepathic communication that two or more people are thinking of
the same idea at the same time?
JC:Yes, because its all happening on the mental plane. Everybodys mind is in
the aphysical dimension.
PJP: Your program
has been highly successful with autism in children as well as a number of other health conditions. Specifically, how does
it work in this regard?
JC:For example - lets say that a person has a painful migraine and has asked
me to hook them up with the technology. Once I've hooked them up, the
technology locates that persons mind which is connected to the physical body
and begins to undo the blocks that were "triggered" by a past event
that was originally responsible for creating the condition that led to the
migraines.
The ADAM process simply
removes the specific block that prevents a person from returning to his or her
original state of health and wholeness, thats all.
PJP: This is
awesome. I know something powerful does, indeed, happen with this technology
because I have experienced it for myself. What other conditions has ADAM been
successful with?
JC:Many of our clients come to us because they have been kicked out by the
medical community as incurable - usually its the ones under pain management. I
dont fault the medical community for this only because doctors scratch their
heads when it comes to conditions like chronic fatigue or fibromyalgia. They
dont have a solution for these conditions other than pain management through
medications.
With conditions of
fibromyalgia, its interesting that 70% of these cases were involved in serious
auto accidents. With the ADAM technology, weve been very successful in that we
can get rid of the pain permanently in just a few days. After that, its a
matter of rebuilding their self-esteem and confidence to get back into the car.
We also have a youthing program thats doing very well now. The results
were seeing is hair growing back, improvement in skin texture, reduction in
wrinkles and so forth.
As per Dr Joe Champion ;
The Mathematical Models of the Portal
To establish a
communication between the Physical Dimension and the Aphysical
Dimension requires the ability to open a Portal within a Dimensional Rift. This
Portal is not singular in nature, but a complex array of doors. The reason that
the Portal has evaded science is that there are no recognizable active
energies. The entrance and exit through the Portal is
based on vibrations. These vibrations (Phonons) occur at an atomic level that
differs from, but does not disagree with, the standard accepted physical model.
Furthermore, this Phononic State does not rely on the
energetic state or charge of the atom.
The Phonon state
is a quiescent model that relates to the diameter of the atom and/or molecule.
As we all are
aware, molecules expand with temperature. To simplify this for the moment, let
us observe this reaction in a singular element. In a singular element, we can
calculate the mechanical spacing by using two formulas. First
we have to calculate the quantity of a given atom for a specific distance. This
calculation is accomplished by the following formula:
whereas:
d = Density in
gm/cm3
Na = Avogadro's
Constant
m = mass
By determining the
inverse, one will observe the linear atomic spacing:
The above is an
important number for it establishes the essence of opening the Portal between
the Dimensions. This formula applies to all known stable isotopes.
Continuing, an element
[or molecule] can open the Portal between the Dimensions only under the
following select conditions. This occurs only when it reaches the Phonon
Resonance of another element [or molecule]. This occurs only by heating or
cooling of the starting element/molecule. Every element and molecule has a distinct Phonon Resonance. However, it is not required
that the second molecule be present in order to open
the Portal. In fact, there are cases wherein a new element will form from the
Phonon Resonance. This is dependant on the side of the Portal where the
energies are focused.
Hence, the portal
is totally energy (temperature) dependant. To determine how an atom [or
molecule] changes its Phonon Resonance with temperature, you must apply certain
standards. For, as a group of like elements are heated or cooled, they will
expand and contract at a given rate. This rate is known as the Expansion
Coefficient [EC]. Another standard is the Standardized Temperature [St]. Thus,
as the temperature rises, the Phonon Resonance will decrease. This is explained
in the following formula.
The last formula
in this series allow us to calculate the exact
temperature wherein a Portal will open based on two known elements
(specifically, the isotopes of the elements).
The application of
this data is of great importance in stabilizing the Portal within the Rift
(Natural or Synthetic).
The opening of a
Portal as it relates to the Human Body is applied from Phononic
Constant of an individual's DNA Code from the Cell Universe.
The above
mathematical formulas provide the basis for the ADAM Technology.
Following is a
typical application in the area of restoring health at
a distance.
When the Operator
of the ADAM Technology connects with the patient by telephone, a Physical
connection is established. Once this occurs and instructions are established
within the computer, a communication can be established between the Operator, ADAM and the Patient. This connection requires the
willingness of a Patient and the concentration of the Operator.

WHATS NEW AND EXCITING AT S.O.S ?
MIA ; Jan Pajak, Joel McClain, Dr Joe Champion,
Michael Heleus,
Gary Whitman, et al



the_sound_of_stars]
Wednesday, August 19, 2009 6:02 PM
From: "Naia
Cumming"
To: the_sound_of_stars@yahoogroups.com
What a shift!
felt quite spaced
out for the next few hours.
The first morning
as I drifted to awakening I could see a pattern in my minds eye like a wormhole
that I thought was
related to the frequencies. I'm seeing
more blue orbs in my visual field
throughout the day
and on and off a wave of heat comes over me.
Thanks Doc!! Looking
forward to your explanation!
Naia
From: "hollydolben"
<holly_dolben@
To:
the_sound_of_stars@yahoogroups.com
I started listening to the mp3
version standing, but within a minute or two the otherwordly sound
of it reached me
inside and I HAD to lie down. I was trying to 'pay attention' to the
effects,
but found myself
feeling like I was going through a worm-hole in outer
space or going into
a deep water space under the ocean somewhere. I
dozed off or went 'out there' for a few minutes.
But about 6-7
minutes in my eyes suddenly flipped open and I felt refreshed.
Now I am noticing a tingling and
light feeling at the sides of my neck and my shoulders. Kudos!
These are great.
Holly
..
LINKS ;
https://www.soundofstars.org/summaryhigher.htm
https://www.soundofstars.org/comments.htm#more
https://www.soundofstars.org/proof.htm#news
https://www.soundofstars.org/miscreports.htm
WHATS NEW AND EXCITING AT S.O.S ?
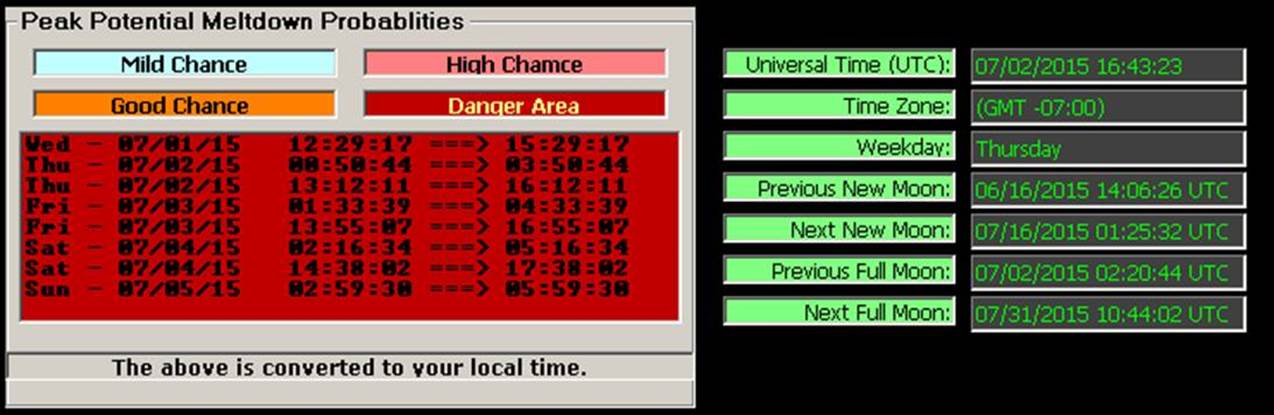
FORECASTING TIMES OF
ILLNESS IN ADVANCE :
WHEN WILL PATIENTS / CLIENTS EXPERIENCE A MELT DOWN OR RESURGENCE OF
SYMPTOMS?
Dr Joe Champion
found that his patients / clients state often clocked to the synodic periods of
the moon.
Something was
happening in relation to a recurring natural background cycle that caused
people to regress.
During these
times operating his technology became more problematic and the positive effects
lessened.
By using his
technology during certain time windows and avoiding usage during other times much
more progress
could be
made. Dr Champion created an entirely
unique and novel software program that would let him accurately
forecast days
in advance, very specific time windows to use or avoid. As a senior member on his team
I was given
this software
and have used it many many times for over 15 years
and have been stunned at how consistently
accurate it has
been.
The Moon Phase Calculator was
originally developed for parents of autistic children. For an
unknown reason, many children with autism have abnormal reactions during the
selective lunar periods. Following is a report that collaborates
this observation.
Data on five aggressive and/or
violent human behaviors were examined by computer to determine whether a
relationship exists between the lunar synodic cycle and human aggression.
Homicides, suicides, fatal traffic accidents, aggravated assaults and
psychiatric emergency room visits occurring in Dade County, Florida all show
lunar periodicities. Homicides and aggravated assaults demonstrate statistically
significant clustering of cases around full moon. Psychiatric emergency room
visits cluster around first quarter and shows a significantly decreased
frequency around new and full moon. The suicide curve shows correlations with
both aggravated assaults and fatal traffic accidents, suggesting a
self-destructive component for each of these behaviors. The existence of a
biological rhythm of human aggression which resonates with the lunar synodic
cycle is postulated.(1)
(1) J Clin Psychiatry. 1978 May;39(5):385-92.

SEE THE FULL
ARCHIVE HERE ;
https://web.archive.org/web/20130112025349/http://paulapeterson.com/Dr_Joe_Champion.html
http://www.rexresearch.com/champion/wo94.htm
https://web.archive.org/web/20110321001352fw_/http://www.drjoechampion.com/attack_pictures.htm
WHATS NEW AND EXCITING AT S.O.S ?
PORTAL SEEN, CREATURE
CRAWLS OUT :

It is here that an entire team of
researchers watched in awe
as a bright door or portal opened up in the darkness and a
large humanoid creature crawled
out before quickly vanishing.
And it is here that several
animals--cattle and dogs--
were mutilated, obliterated or simply disappeared.
http://soundofstars.org/portalseen.htm
PLASMA MIND :

http://soundofstars.org/plasmamind.htm
WHATS NEW AND EXCITING AT S.O.S ?
THOUGHT IS
ELECTRIC, EMOTION IS MAGNETIC
THE NATURE OF THOUGHT :

https://youtu.be/o2FD3W7sOBk?t=308
The phase, distinct
from the energy, can travel faster than light.
Professor Emilio Del Giudice:
WHATS NEW AND EXCITING AT S.O.S ?
NEW ARTICLES
AVAILABLE
RECENT ( CURRENT ) ;
DNA REGENERATION
: INCREASING THE LENGTH OF TELOMERES
ANTI-AGING EXOTIC CUTTING
EDGE TECHNOLOGIES
QUANTUM
BIOLOGY & THE SECRET OF BLUE LIGHT
SEE
FULL ARTICLE ; https://soundofstars.org/quantumbiology.htm
Dr.
Mae-Wan Ho proved that molecules of life are based on resonant quantum coherent
energy transfer, emitting biophotons, each of us has a spirit inside us!
birefringent, liquid crystalline order gives off the coherent biophotons.
"The
most coherent parts are the most active parts, showing up in the organism as
those with the brightest colours. (We've done all the physics and mathematics
to prove that's the case.) And when the organism dies, the colours fade as
random thermal motions takes over." Dr. Mae-Wan Ho
human
adult stem cells and human somatic (non-stem) cells can be reprogrammed back to
an embryonic-like state with electromagnetic fields and sound.
The
melodies entailed within the sound of a heartbeat, or the vibrations within the
Actors words will talk to human stem cells on the stage, to reprogram them to
an Ancient ancestral state, like the embryonic one when they were capable of
doing everything, disclosing a portal to the Future of Art and human
wellbeing."
Our
cells generate a seeming infinity of vibrations and sounds that tell of their
healthy or diseased state.
SEE
FULL ARTICLE ; https://soundofstars.org/quantumbiology.htm
-
GENETIC KEYS to Spirituality : CD38 & VMAT2
https://soundofstars.org/godgene.htm
.
CAUSES & TREATMENT METHODS FOR ALS LOU
GEHRIGS DISEASE,
DEMENTIA, ALZHEIMERS, STROKE LIKE INCIDENT
These documents outline key considerations
for the three main health issues of ;
ALS LOU GEHRIGS DISEASE
DEMENTIA / ALZHEIMERS
STROKE LIKE INCIDENT
ALS METHODS
https://soundofstars.org/alsmethods.htm
ALS CAUSES
https://soundofstars.org/alscause.htm
.
REPLICATING
MOLECULAR MAGNETIC FIELDS
https://soundofstars.org/replicatingfields.htm
FREQUENCIES
OF THE GEOMETRY OF MIND
https://soundofstars.org/frequenciesofmind.htm
FREQUENCIES
OF NEUROBIOLOGICAL RESONANCES & CEREBRAL BREATHING
https://soundofstars.org/enzymefrequencies.htm
USING
SOUND TO CONTROL ENZYMATIC REACTIONS
https://soundofstars.org/enzymefrequencies.htm
ELECTROMAGNETIC
PATTERNS OF CONSCIOUS ENERGY
https://soundofstars.org/consciousenergy.htm
ALUMINUM:
HOW TO REMOVE WITH SILICA
https://soundofstars.org/aluminumremoval.htm
NEW
- FREQUENCIES OF ATOMS
-
TRANSFORMING THE SPECTRAL LINES OF EACH ELEMENT INTO A MUSICAL TONE
https://soundofstars.org/atomsongs.htm
The Fourier Transform in Your Eyes
the
lens took rays that were global and made them local.
the phase is where you are in the cycle of the wave: are
you in a peak, a trough, the middle,
etc. But for
this derivation, just know that its the stuff to goes into the exponent of the
complex
exponential.

The transform is fundamental tool in
science, but also is how your eyes see the world.
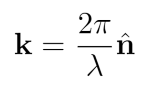 Equation 2: the wavevector definition, where
the unit vector n points in the
Equation 2: the wavevector definition, where
the unit vector n points in the
direction
of propagation. λ is the wavelength of light. where n is a unit vector pointing along
the ray.
Because of the k-label, its also standard
to call these k-vectors. This is the k goes into our wave
function exp(ikr).
https://www.cantorsparadise.com/the-fourier-transform-in-your-eyes-84cfe0fa31b4
PETER
KINGSLEY: Parmenides and Empedocles lived just before the time in Western
history when, with Plato and the influence of Aristotles disciples, we start
to get the general notion that the senses lie. And because of this idea they
were completely misunderstood.
P: So this is not a new idea.
PK: No, no. Its implicit even before Plato, and later Greek philosophers
formulate it very clearly: the senses are liars. Now Empedocles also begins his
teaching poem by saying that the senses lead people astray. And so does
Parmenides before him. But people dont really read what they say. Instead they think: well, Parmenides and Empedocles tell us
the senses are unreliable therefore we have to find truth through some other
means.
It sounds
very logical. The trouble is Empedocles and Parmenides never said that. What
they said is that the senses aswe know
them are unreliable, because we were never taught how to use them.
Empedocles in particular was very specific. He
explained that our senses are still closed. For him, we humans are plants:
human plants. Actually we are seeds and have not yet
become plants. We have not budded yet, have not yet started to open and blossom. We have the potential to become full human
beings but the potential has not been realized. And I
find this amazing and terrifying, that someone 2,500 years agosomeone who was
laying the foundations for all our philosophical and scientific
disciplinessaid were not yet human, because what he said then applies just as
much to us today.
https://parabola.org/2016/11/01/common-sense-an-interview-with-peter-kingsley/
WHATS NEW AND EXCITING AT S.O.S ?
ACCESS YOUR FREE FREQUENCIES AT THIS LINK ;
http://soundofstars.org/welcome/
LEARN MORE ABOUT US ;
GUEST APPEARANCE ON RADIO SHOW
SCIENCE OF PEAK PERFORMANCE & VIBRATIONAL WELLNESS
;
QUANTUM CONVERSATIONS SHOW WITH LAUREN GALEY -
PART 1
https://www.youtube.com/watch?v=QvIgtvzi6Nk
QUANTUM CONVERSATIONS SHOW WITH LAUREN GALEY -
PART 2
Cymatherapy LAUREN GALEY SHOW PART 2 - QUANTUM CONVERSATIONS cymatics cymatic therapy frequencies
COPYRIGHT
PROTECTION NOTICE, ALL RIGHTS RESERVED WORLD WIDE BY
DONALD
ADAMS, 2007 to 2018. READ BEFORE ACCESSING AND USING
These
files are for your personal use and protection and for your family.
ALL
CONTENT IS COPY RIGHT PROTECTED AND MAY NOT BE DUPLICATED,
REDISTRIBUTED,
EXHIBITED, INCORPORATED IN ANY WAY WITHOUT PRIOR
EXPRESS
PERMISSION FROM DONALD ADAMS, THE DEVELOPER. AN EXAMPLE
OF THIS
WOULD BE, IF YOU ARE A DJ YOU MAY NOT INCORPORATE
OUR
CONTENT
IN THE PRODUCTION OF ENTERTAINMENT CONTENT FOR YOUR AUDIENCE.
HEALTH
AND WELLNESS PRACTITIONERS MAY NOT USE ANY 'SOUND OF STARS'
FREQUENCIES
( INCLUDING THE CONTENT IN THIS VIDEO) IN THEIR
PRACTICE FOR
CLIENTS
WHERE A COMMERCIAL TRANSACTION IS OCCURRING IN ASSOCIATION
WITH
OUR CONTENT WITHOUT FIRST PAYING FOR A USAGE LICENSE OR WITHOUT
PRIOR
PERMISSION FROM THE DEVELOPER. AN EXAMPLE OF THIS IS, IF YOU ARE
PROVIDING
MASSAGE THERAPY FOR A FEE TO A CLIENT AND YOU ARE USING
OUR
CONTENT IN THE BACK GROUND WHILE YOU PROVIDE THE
SERVICE
- THIS
SORT OF SCENARIO IS A BREACH OF OUR USAGE TERMS AND IS PROHIBITED -
YOU
MUST FIRST SEEK EXPLICIT PERMISSIONS AND LICENSING PRIOR.
All
files are copyright protected and may not be shared or redistributed to others
and are strictly for your own personal use
Disclaimer: None
of the information provided on this site or on this page-including information
provided in any videos or reviews expressed by individuals or other third
parties- is intended to communicate any medical information, and no products or
devices described are natural health products or medical devices. For a full
summary of the intended use of any products sold on this site, as well as more
clarity on why none of our products are to be used for health related or
medical purposes, (especially not as medical devices or health products),
please carefully read through all of our disclaimers
listed. To read all of our full disclaimers click
here.
Video Disclaimer: Thank you for
watching our video. Please note that all the information and views provided in
this video is not to be construed as advice, and such information constitutes
only the opinion of the presenter or individual expressing or communicating the
information. We (Sound of Stars Frequencies - Donald Adams )
do not endorse, vouch for or encourage any of the opinions or views of those
presenting information in this video, and such views belong only to those
making them. Furthermore, we do not endorse or assert the reliability,
accuracy, fitness for any purpose or truth of any information, products, services or statements shown in our video, and we expect
that you, the viewer, will make a researched, personally informed and
independent evaluation as to the truthfulness of any information presented in
this video. Do also note that any device described in this video is not a
medical device under any circumstances unless explicitly stated. Therefore, any
such devices shown in our video are not displayed to cure, treat
or remedy any health condition or illness. For any matters related to your
health, do ensure that you consult your doctor for proper diagnoses and
treatment. Any consumable products displayed in this video are also not
regulated or approved by any regulatory agency, and therefore you should fully
research the nature and contents of such products, as well as their regulated
status in the region you reside, before taking any decision to obtain, use or
purchase such products.